
分析 (1)假设f(x)=sinx是“可平衡”函数,由题意$\sqrt{3}$sinx=sin(x+k)+sin(x-k),由此求出m、k的值;
(2)由题意求出m1、m2的值,利用m1+m2=a,结合三角函数的图象与性质求出a 的取值范围.
解答 解:(1)假设f(x)=sinx是“可平衡”函数,则由题意应有:
$\sqrt{3}$sinx=sin(x+k)+sin(x-k)
=sinxcosk+cosxsink+sinxcosk-cosxsink
=2sinxcosk;
∴cosk=$\frac{\sqrt{3}}{2}$,解得 k=2tπ±$\frac{π}{6}$,t∈Z;
∴存在实数m、k(m≠0),使得对于定义域内的任意实数x,
均有m•f(x)=f(x+k)+f(x-k)成立;
∴f(x)=sinx是“可平衡”函数,
且 $cosk=\frac{{\sqrt{3}}}{2}∴k=±\frac{π}{6}+2nπ,n∈Z$;
(2)由题意m1sin2x=sin2(x+$\frac{π}{2}$)+sin2(x-$\frac{π}{2}$)=2cos2x,
∴m1=$\frac{{2cos}^{2}x}{{sin}^{2}x}$;
m2sin2x=sin2(x+$\frac{π}{4}$)+sin2 (x-$\frac{π}{4}$)=sin2(x+$\frac{π}{4}$)+cos2(x+$\frac{π}{4}$)=1,
解得m2=$\frac{1}{{sin}^{2}x}$;
∴m1+m2=$\frac{{2cos}^{2}x+1}{{sin}^{2}x}$=$\frac{2cos2x+4}{1-cos2x}$=a,
解得cos2x=$\frac{a-4}{a+2}$,
∵0<x<$\frac{π}{3}$,∴0<2x<$\frac{2π}{3}$,
∴-$\frac{1}{2}$<cos2x<1,且y=cos2x是单调递减,
∴方程m1+m2=a不会有两个不相等的实根,即a的取值范围为∅.
点评 本题考查了三角函数的图象与性质的应用问题,也考查了函数与方程的应用问题,是综合题.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:解答题
已知直线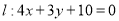 ,半径为
,半径为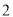 的圆
的圆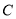 与
与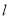 相切,圆心
相切,圆心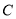 在
在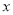 轴上且在直线
轴上且在直线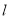 的右上方.
的右上方.
(1)求圆的方程;
(2)若直线过点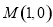 且与圆
且与圆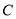 交于
交于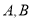 两点(
两点(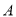 在
在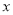 轴上方,B在
轴上方,B在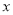 轴下方),问在
轴下方),问在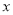 轴正半轴上是否存在定点
轴正半轴上是否存在定点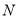 ,使得
,使得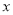 轴平分
轴平分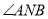 ?若存在,请求出点
?若存在,请求出点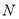 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 组号 | 分组 | 频数 |
| 1 | [53,61) | 5 |
| 2 | [61,69) | 14 |
| 3 | [69,77) | 25 |
| 4 | [77,85) | 11 |
| 5 | [85,93) | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{9}$ | B. | $\frac{7}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{8}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小正周期是π | B. | 区间[0,2]上的增函数 | ||
| C. | 图象关于点(kπ,0)(k∈Z)对称 | D. | 周期函数且图象有无数条对称轴 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com