
| A. | 最小正周期是π | B. | 区间[0,2]上的增函数 | ||
| C. | 图象关于点(kπ,0)(k∈Z)对称 | D. | 周期函数且图象有无数条对称轴 |
分析 化简函数f(x),根据函数的图象与性质判断四个选项是否正确即可.
解答 解:函数f(x)=cosx+|cosx|
=$\left\{\begin{array}{l}{2cosx,x∈[-\frac{π}{2}+2kπ,\frac{π}{2}+2kπ],k∈Z}\\{0,x∈(\frac{π}{2}+2kπ,\frac{π}{2}+\frac{3π}{2}+2kπ),k∈Z}\end{array}\right.$,
∴f(x)是周期函数,且最小正周期为2π,A错误;
∵2>$\frac{π}{2}$,∴x∈[0,2]时,f(x)不是增函数,B错误;
f(x)的图象不关于点(kπ,0)(k∈Z)对称,C错误;
f(x)是周期函数且图象有无数条对称轴为x=kπ,k∈Z,D正确.
故选:D.
点评 本题考查了余弦函数的图象与性质的应用问题,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>n | B. | m<n | C. | m=n | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:解答题
(1)用辗转相除法求228与1995的最大公约数.
(2)用秦九韶算法求多项式f(x)=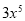 +
+ -8x+5在x=2时的值。
-8x+5在x=2时的值。
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:填空题
直线l1和l2是圆x2+y2=2的两条切线.若l1与l2的交点为(1,3),则l1与l2的夹角的正切值等于________
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com