
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 先对两个函数分析可知,函数f(x)与g(x)都是奇函数,且f(x)是反比例函数,g(x)在[0,π]上是减函数,在[π,2π]上是增函数,在[2π,3π]上是减函数,且g(0)=0,g(π)=-π;g(2π)=2π;g(3π)=-3π;从而作出函数的图象,由图象求方程的根的个数即可.
解答 解:g′(x)=cosx-xsinx-cosx=-xsinx;
令g′(x)=0得x=kπ,k∈Z.
∴g(x)在[0,π]上是减函数,在[π,2π]上是增函数,在[2π,3π]上是减函数,
且g(0)=0,g(π)=-π;g(2π)=2π;g(3π)=-3π;
故作函数f(x)与g(x)在[0,3π]上的图象如下,
结合图象可知,两图象在[0,3π]上共有3个交点;
又f(x),g(x)都是奇函数,且f(x)不经过原点,
∴f(x)与g(x)在[-3π,3π]上共有6个交点,故f(x)=g(x)有6个零点.
故选C.
点评 本题考查了导数的综合应用及函数的图象的性质应用,同时考查了函数的零点与方程的根的关系应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 最小正周期是π | B. | 区间[0,2]上的增函数 | ||
| C. | 图象关于点(kπ,0)(k∈Z)对称 | D. | 周期函数且图象有无数条对称轴 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:选择题
以下四个命题中:
①在回归分析中, 可用相关指数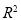 的值判断的拟合效果,
的值判断的拟合效果,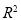 越大,模型的拟合效果越好;
越大,模型的拟合效果越好;
②两个随机变量的线性相关性越强,相关系数的绝对值越接近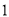 ;
;
③若数据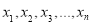 的方差为
的方差为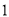 ,则
,则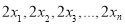 的方差为
的方差为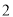 ;
;
④对分类变量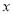 与
与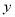 的随机变量
的随机变量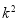 的观测值
的观测值 来说,
来说,  越小,判断“
越小,判断“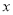 与
与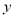 有关系”的把握程度越大.
有关系”的把握程度越大.
其中真命题的个数为( )
A.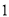 B.
B.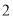 C.
C.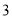 D.
D.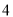
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川省高二上学期期中考数学试卷(解析版) 题型:选择题
若直线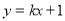 与圆
与圆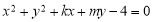 交于
交于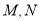 两点,且
两点,且 关于直线
关于直线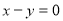 对称,动点P
对称,动点P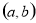 在不等式组
在不等式组 表示的平面区域内部及边界上运动,则
表示的平面区域内部及边界上运动,则 的取值范围是( )
的取值范围是( )
A.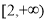 B.
B.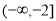
C. D.
D.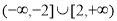
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com