
分析 当x+2>0时,f(x+2)=1;x+2<0时,f(x+2)=-1,对x进行分类讨论后代入原不等式即可求出不等式的解集.
解答 解:∵不等式x+(x+2)f(x+2)≤5,
∴x+2+(x+2)f(x+2)≤7,
当x+2>0时,f(x+2)=1,代入原不等式得:x+2+x+2≤7⇒-2<x≤$\frac{3}{2}$;
当x+2<0时,f(x+2)=-1,代入原不等式得:x+2-x-2≤7⇒0≤7,即x<-2;
综上,原不等式的解集为(-∞,-2)∪(2,$\frac{3}{2}$].
故答案为:(-∞,-2)∪(2,$\frac{3}{2}$].
点评 此题考查了分段函数、不等式的解法,考查了分类讨论的数学思想,是一道基础题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
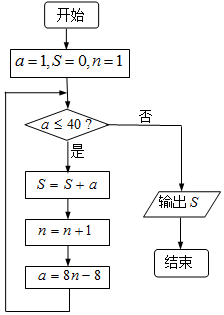 《孙子算经》是我国古代的数学著作,其卷下中有类似如下的问题:“今有方物一束,外周一匝有四十枚,问积几何?”如右图是解决该问
《孙子算经》是我国古代的数学著作,其卷下中有类似如下的问题:“今有方物一束,外周一匝有四十枚,问积几何?”如右图是解决该问| A. | 81 | B. | 74 | C. | 121 | D. | 169 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0] | B. | (-∞,0]∪{$\frac{2}{e}$} | C. | (-∞,$\frac{2}{e}$) | D. | (-∞,$\frac{2}{e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com