
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
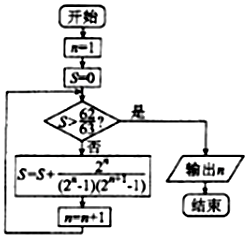
分析 由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量n的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解答 解:由于$\frac{{2}^{n}}{({2}^{n}-1)({2}^{n+1}-1)}$=$\frac{1}{{2}^{n}-1}$-$\frac{1}{{2}^{n+1}-1}$,
由题意可得:S=(1-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{7}$)+…+$\frac{1}{{2}^{n}-1}$-$\frac{1}{{2}^{n+1}-1}$=1-$\frac{1}{{2}^{n+1}-1}$>$\frac{62}{63}$,
解得:n>5,即累加项大于5,
由程序框图,当n=5时,应该不满足条件S>$\frac{62}{63}$,执行循环体,计算S的值,n=6
应该不满足条件S>$\frac{62}{63}$,执行循环体,计算S的值,n=7,
此时,应该满足条件S>$\frac{62}{63}$,退出循环,输出n的值为7.
故选:C.
点评 本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川省高二上学期期中考数学试卷(解析版) 题型:选择题
如果两条直线l1: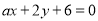 与l2:
与l2: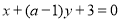 平行,那么a等于( )
平行,那么a等于( )
A.1 B.-1 C.2 D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 110 | B. | 120 | C. | 130 | D. | 140 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>c>a | C. | a>c>b | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{3}$ | B. | $-\frac{24}{7}$ | C. | $\frac{24}{7}$ | D. | $\frac{24}{25}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com