
���� ����i��f��x���Ķ�����Ϊ{x|x��0}��f�䣨x��=1+lnx��g�䣨x��=ax+1����m=eʱ��f�䣨e��=1+lne=2��g�䣨e��=ae+1����l1��l2�����õ����ļ��������f�䣨e��g�䣨e��=2��ae+1��=-1���ɴ������a��
��ii��f�䣨m��=1+lnm��g�䣨m��=am+1����l1��l2����lnm=am�ڣ�0��+�ޣ����н⣬�Ӷ�a=$\frac{lnm}{m}$����F��x��=$\frac{lnx}{x}$��x��0������${F}^{'}��x��=\frac{1-lnx}{{x}^{2}}$=0����x=e�����õ����������F��x��max=F��e��=$\frac{1}{e}$���ɴ������a�����ֵ��
����h��x��=xlnx-$\frac{a}{2}{x}^{2}$-x+a����x��0����h�䣨x��=lnx-ax���Ӷ�x1��x2�Ƿ���lnx-ax=0��������������a=$\frac{ln{x}_{1}-ln{x}_{2}}{{x}_{1}-{x}_{2}}$���Ƶ���$\frac{ln{x}_{1}-ln{x}_{2}}{{x}_{1}-{x}_{2}}$��$\frac{1+��}{{x}_{1}+��{x}_{2}}$���Ӷ�ln$\frac{{x}_{1}}{{x}_{2}}$��$\frac{��1+�ˣ���{x}_{1}-{x}_{2}��}{{x}_{1}+��{x}_{2}}$����t=$\frac{{x}_{1}}{{x}_{2}}$����t�ʣ�0��1�����Ӷ�lnt��$\frac{��1+�ˣ���t-1��}{t+��}$��t�ʣ�0��1���Ϻ��������գ�t��=lnt-$\frac{��1+�ˣ���t-1��}{t+��}$����ա䣨t��=$\frac{1}{t}-\frac{��1+�ˣ�^{2}}{��t+�ˣ�^{2}}$=$\frac{��t-1����t-{��}^{2}��}{t��t+�ˣ�^{2}}$���ɴ˸��ݦ�2��1�ͦ�2��1�������ۣ����õ�������������˵�ȡֵ��Χ��
��� �⣺����i���ߺ���f��x��=xlnx����f��x���Ķ�����Ϊ{x|x��0}��f�䣨x��=1+lnx��
��g��x��=$\frac{a}{2}{x^2}$+x-a��a��R������g�䣨x��=ax+1��
��m=eʱ��f�䣨e��=1+lne=2��g�䣨e��=ae+1��
��l1��l2����f�䣨e��g�䣨e��=2��ae+1��=-1��
���a=-$\frac{3}{2e}$��
��ii���ߺ���f��x��=xlnx����f��x���Ķ�����Ϊ{x|x��0}��f�䣨x��=1+lnx��
��g��x��=$\frac{a}{2}{x^2}$+x-a��a��R������g�䣨x��=ax+1��
��f�䣨m��=1+lnm��g�䣨m��=am+1��
��l1��l2����f�䣨m��=g�䣨m���ڣ�0��+�ޣ����н⣬
��lnm=am�ڣ�0��+�ޣ����н⣬
��m��0����a=$\frac{lnm}{m}$��
��F��x��=$\frac{lnx}{x}$��x��0������${F}^{'}��x��=\frac{1-lnx}{{x}^{2}}$=0�����x=e��
��x�ʣ�0��e��ʱ��F�䣨x����0��F��x��Ϊ��������
��x�ʣ�e��+�ޣ�ʱ��F�䣨x����0��F��x��Ϊ��������
��F��x��max=F��e��=$\frac{1}{e}$��
��a�����ֵΪ$\frac{1}{e}$��
����h��x��=xlnx-$\frac{a}{2}{x}^{2}$-x+a����x��0����h�䣨x��=lnx-ax��
��x1��x2Ϊh��x�����䶨�����ڵ�������ͬ�ļ�ֵ�㣬
��x1��x2�Ƿ���lnx-ax=0������������lnx1=ax1��lnx2=ax2��
��ʽ������������ã�a=$\frac{ln{x}_{1}-ln{x}_{2}}{{x}_{1}-{x}_{2}}$��
�ߦˣ�0��0��x1��x2��
�ɦ�lnx2-�ˣ�1-lnx1����1+�ˣ�lnx1+��lnx2��
��1+�ˣ�a��x1+��x2������a��$\frac{1+��}{{x}_{1}+��{x}_{2}}$����$\frac{ln{x}_{1}-ln{x}_{2}}{{x}_{1}-{x}_{2}}$��$\frac{1+��}{{x}_{1}+��{x}_{2}}$��
��ln$\frac{{x}_{1}}{{x}_{2}}$��$\frac{��1+�ˣ���{x}_{1}-{x}_{2}��}{{x}_{1}+��{x}_{2}}$��
��t=$\frac{{x}_{1}}{{x}_{2}}$����t�ʣ�0��1����������֪��
lnt��$\frac{��1+�ˣ���t-1��}{t+��}$��t�ʣ�0��1���Ϻ������
��գ�t��=lnt-$\frac{��1+�ˣ���t-1��}{t+��}$����ա䣨t��=$\frac{1}{t}-\frac{��1+�ˣ�^{2}}{��t+�ˣ�^{2}}$=$\frac{��t-1����t-{��}^{2}��}{t��t+�ˣ�^{2}}$��
�ٵ���2��1ʱ�����ˡ�1ʱ��?t�ʣ�0��1�����ա䣨t����0��
��գ�t���ڣ�0��1���ϵ���������
�֦գ�1��=0����գ�t����0�ڣ�0��1���Ϻ������
�ڵ���2��1����0���ˣ�1ʱ��t�ʣ�0����2��ʱ���ա䣨t����0���գ�t���ڣ�0����2��������������
��t�ʣ���2��1��ʱ���ա䣨t����0���գ�t���ڣ���2��1�����Ǽ�������
�֦գ�1��=0����գ�t������С��0���������⣮
���ϣ��˵�ȡֵ��Χ��[1��+�ޣ���
���� ���⿼�鵼���ļ������塢�������ʡ����취���������ʵȻ���֪ʶ������������֤����������������������黯����ת��˼�롢����������˼�룬���鴴����ʶ��Ӧ����ʶ�����е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ��ӱ�ʡ�߶����ϵ�һ���¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
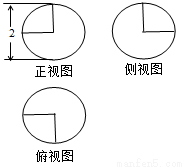
һ�����徭���и��ʣ�²��ּ����������ͼ����ͼ��ʾ����ʣ�²��ּ���������Ϊ�� ��
A��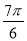 B��
B��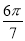 C��
C��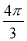 D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1-i | B�� | 1+i | C�� | 2-2i | D�� | 2+2i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | i | D�� | -i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
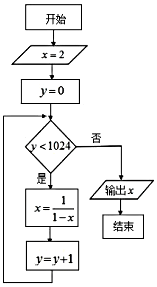
| A�� | 2016 | B�� | 1024 | C�� | $\frac{1}{2}$ | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\lim_{n����}{a_n}$��$\lim_{n����}{S_n}$������ | B�� | $\lim_{n����}{a_n}$��$\lim_{n����}{S_n}$�������� | ||
| C�� | $\lim_{n����}{a_n}$���ڣ�$\lim_{n����}{S_n}$������ | D�� | $\lim_{n����}{a_n}$�����ڣ�$\lim_{n����}{S_n}$���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com