
分析 先判断函数f(x)的对称性,再判断g(x)的奇偶性和单调区间,化简不等式解得即可.
解答 解:∵函数f(x)对?x∈R满足f(x)=-f(2-x),∴f(x)的图象关于点(1,0)对称.
∵g(x)=f(1+x),f(x)在[1,+∞)上递增,
∴g(x)为奇函数,并且在[0,+∞)是增函数.
∵2g(log2a)-3g(1)≤g(log${\;}_{\frac{1}{2}}$a)=g(-log2a)=-g(log2a),
∴3g(log2a)≤3g(1)
即log2a≤1=log22,∴0<a≤2,
故答案为:(0,2].
点评 本题考查了函数的奇偶性和单调性的综合应用,注意自变量的取值范围,考查了学生的转化能力,属于中档题.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [-2,1] | B. | [-2,2] | C. | [-2,3] | D. | [-2,4] |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川省高二上学期期中考数学试卷(解析版) 题型:选择题
如果两条直线l1: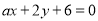 与l2:
与l2: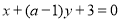 平行,那么a等于( )
平行,那么a等于( )
A.1 B.-1 C.2 D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 110 | B. | 120 | C. | 130 | D. | 140 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com