
分析 (1)利用组合数公式直接计算;
(2)根据(1)的计算猜想公式,根据组合数的性质进行化简,将条件向假设式配凑得出.
解答 解:(1)f1(x)=${C}_{1}^{0}$x-${C}_{1}^{1}$(x-1)=x-x+1=1,
f2(x)=${C}_{2}^{0}{x}^{2}$-${C}_{2}^{1}(x-1)^{2}$+${C}_{2}^{2}(x-2)^{2}$=x2-2(x2-2x+1)+(x2-4x+4)=2,
f3(x)=${C}_{3}^{0}$x3-${C}_{3}^{1}$(x-1)3+${C}_{3}^{2}$(x-2)2-${C}_{3}^{3}$(x-3)3=x3-3(x-1)3+3(x-2)3-(x-3)3=6,
(2)猜想:fn(x)=n!.
证明:①当n=1时,猜想显然成立;
②假设n=k时猜想成立,即fk(x)=Ck0xk-Ck1(x-1)k+${C}_{k}^{2}$(x-2)k+…+(-1)kCkk(x-k)k=k!,
则n=k+1时,fk(x)=C${\;}_{k+1}^{0}$xk+1-${C}_{k+1}^{1}$(x-1)k+1+C${\;}_{k+1}^{2}$(x-2)k+1+…+(-1)k+1C${\;}_{k+1}^{k+1}$(x-k-1)k+1
=xC${\;}_{k+1}^{0}$xk-(x-1)${C}_{k+1}^{1}$(x-1)k+(x-2)C${\;}_{k+1}^{2}$(x-2)k+…+(-1)k(x-k)${C}_{k+1}^{k}$(x-k)k+(-1)k+1C${\;}_{k+1}^{k+1}$(x-k-1)k+1
=x[C${\;}_{k+1}^{0}$xk-${C}_{k+1}^{1}$(x-1)k+C${\;}_{k+1}^{2}$(x-2)k+…+(-1)k(x-k)${C}_{k+1}^{k}$(x-k)k]
+[${C}_{k+1}^{1}$(x-1)k-2C${\;}_{k+1}^{2}$(x-2)k+…+(-1)kk${C}_{k+1}^{k}$(x-k)k]+(-1)k+1C${\;}_{k+1}^{k+1}$(x-k-1)k+1
=x[C${\;}_{k}^{0}$xk-(${C}_{k}^{0}$+${C}_{k}^{1}$)(x-1)k+(${C}_{k}^{1}{+C}_{k}^{2}$)(x-2)k+…+(-1)k(${C}_{k}^{k-1}$+${C}_{k}^{k}$)(x-k)k]
+(k+1)[${C}_{k}^{0}$(x-1)k-${C}_{k}^{1}$(x-2)k…+(-1)k+1${C}_{k}^{k-1}$(x-k)k]+(-1)k+1C${\;}_{k+1}^{k+1}$(x-k-1)k+1
=x[${C}_{k}^{0}$xk-Ck1(x-1)k+${C}_{k}^{2}$(x-2)k+…+(-1)kCkk(x-k)k]-x[${C}_{k}^{0}$(x-1)k+${C}_{k}^{1}$(x-2)k+…+(-1)k-1Ckk-1(x-k)k+(-1)kC${\;}_{k}^{k}$(x-k-1)k]
+(k+1)[(x-1)k-${C}_{k}^{1}$(x-2)k…+(-1)k+1${C}_{k}^{k-1}$(x-k)k+(-1)k(x-k-1)k]
=xk!-xk!+(k+1)k!
=(k+1)!.
∴当n=k+1时,猜想成立.
点评 本题考查了组合数公式的性质,数学归纳法证明,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | [-4,-2] | B. | [-2,6] | C. | [0,8] | D. | [2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
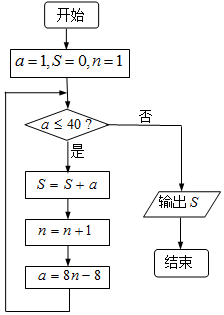 《孙子算经》是我国古代的数学著作,其卷下中有类似如下的问题:“今有方物一束,外周一匝有四十枚,问积几何?”如右图是解决该问
《孙子算经》是我国古代的数学著作,其卷下中有类似如下的问题:“今有方物一束,外周一匝有四十枚,问积几何?”如右图是解决该问| A. | 81 | B. | 74 | C. | 121 | D. | 169 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com