
| A. | $\lim_{n→∞}{a_n}$和$\lim_{n→∞}{S_n}$都存在 | B. | $\lim_{n→∞}{a_n}$和$\lim_{n→∞}{S_n}$都不存在 | ||
| C. | $\lim_{n→∞}{a_n}$存在,$\lim_{n→∞}{S_n}$不存在 | D. | $\lim_{n→∞}{a_n}$不存在,$\lim_{n→∞}{S_n}$存在 |
分析 推导出Sn=2017-($\frac{1}{3}$)n-2016,根据极限的定义即可判断.
解答 解:∵数列{an},对任意的正整数n,an=$\left\{\begin{array}{l}{1,1≤n≤2016}\\{2•(\frac{1}{3})^{n-2016},n≥2017}\end{array}\right.$,设Sn表示数列{an}的前n项和,
∴a1=a2=a3=…=a2016=1,a2017=-$\frac{2}{3}$,a2018=-$\frac{2}{9}$,a2019=-$\frac{2}{27}$,…,
∴Sn=2016+$\frac{\frac{2}{3}[1-(\frac{1}{3})^{n-2016}]}{1-\frac{1}{3}}$=2016+1-($\frac{1}{3}$)n-2016=2017-($\frac{1}{3}$)n-2016,
$\lim_{n→∞}{S_n}$=$\underset{lim}{n→∞}$[2017-($\frac{1}{3}$)n-2016]=2017,$\lim_{n→∞}{a_n}$=$\underset{lim}{n→∞}$(2×($\frac{1}{3}$)n-2016)=0,
故选:A
点评 本题考查了分组求和和极限的定义,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{3}$ | B. | $-\frac{24}{7}$ | C. | $\frac{24}{7}$ | D. | $\frac{24}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x=\frac{π}{6}$ | B. | $x=\frac{π}{3}$ | C. | $x=\frac{5π}{12}$ | D. | $x=\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
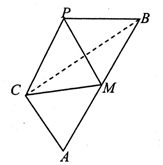 已知△ABC中,∠C=90°,tanA=$\sqrt{2}$,M为AB的中点,现将△ACM沿CM折成三棱锥P-CBM,当二面角P-CM-B大小为60°时,$\frac{AB}{PB}$=$\sqrt{3}$.
已知△ABC中,∠C=90°,tanA=$\sqrt{2}$,M为AB的中点,现将△ACM沿CM折成三棱锥P-CBM,当二面角P-CM-B大小为60°时,$\frac{AB}{PB}$=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com