
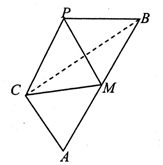
 已知△ABC中,∠C=90°,tanA=$\sqrt{2}$,M为AB的中点,现将△ACM沿CM折成三棱锥P-CBM,当二面角P-CM-B大小为60°时,$\frac{AB}{PB}$=$\sqrt{3}$.
已知△ABC中,∠C=90°,tanA=$\sqrt{2}$,M为AB的中点,现将△ACM沿CM折成三棱锥P-CBM,当二面角P-CM-B大小为60°时,$\frac{AB}{PB}$=$\sqrt{3}$. 分析 由题意画出图形,找出二面角P-CM-B的平面角,设AC=2,求解三角形得答案.
解答 解:如图,取BC中点E,连接AE,设AE∩CM=O,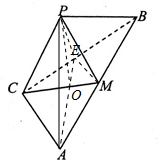
再设AC=2,由∠C=90°,tanA=$\sqrt{2}$,可得BC=$2\sqrt{2}$,
在Rt△MEC中,可得tan$∠CME=\sqrt{2}$,在Rt△ECA中,求得tan$∠AEC=\frac{\sqrt{2}}{2}$,
∴cot∠AEM═$\frac{\sqrt{2}}{2}$,则∠CME+∠AEM=90°,有AE⊥CM.
∴PO⊥CM,EO⊥CM,∠POE为二面角P-CM-B的平面角为60°,
∵AE=$\sqrt{{2}^{2}+(\sqrt{2})^{2}}=\sqrt{6}$,OE=1×sin∠CME=$\frac{\sqrt{6}}{3}$,∴PO=$\frac{2\sqrt{6}}{3}$.
在△POE中,由余弦定理可得PE=$\sqrt{(\frac{2\sqrt{6}}{3})^{2}+(\frac{\sqrt{6}}{3})^{2}-2×\frac{2\sqrt{6}}{3}×\frac{\sqrt{6}}{3}×\frac{1}{2}}$=$\sqrt{2}$.
∴PE2+CE2=PC2,即PE⊥BC.
则PB=PC=2.
在Rt△ACB中,求得AB=2$\sqrt{3}$,
∴$\frac{AB}{PB}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查二面角的平面角及其求法,考查空间想象能力和思维能力,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\lim_{n→∞}{a_n}$和$\lim_{n→∞}{S_n}$都存在 | B. | $\lim_{n→∞}{a_n}$和$\lim_{n→∞}{S_n}$都不存在 | ||
| C. | $\lim_{n→∞}{a_n}$存在,$\lim_{n→∞}{S_n}$不存在 | D. | $\lim_{n→∞}{a_n}$不存在,$\lim_{n→∞}{S_n}$存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
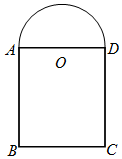 设计人员要用10米长的材料(材料的宽度不计)建造一个窗子的边框,如图所示,窗子是由一个矩形ABCD和以AD为直径的半圆组成,窗子的边框不包括矩形的AD边,设半圆的半径为OA=r(米),窗子的透光面积为S(平方米).
设计人员要用10米长的材料(材料的宽度不计)建造一个窗子的边框,如图所示,窗子是由一个矩形ABCD和以AD为直径的半圆组成,窗子的边框不包括矩形的AD边,设半圆的半径为OA=r(米),窗子的透光面积为S(平方米).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
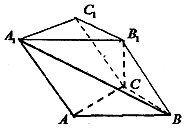 如图,斜三棱柱ABC-A1B1C1中,侧面AA1B1B为菱形,底面△ABC是等腰直角三角形,∠BAC=90°,A1B⊥B1C.
如图,斜三棱柱ABC-A1B1C1中,侧面AA1B1B为菱形,底面△ABC是等腰直角三角形,∠BAC=90°,A1B⊥B1C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com