
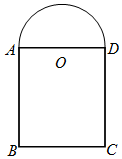
 设计人员要用10米长的材料(材料的宽度不计)建造一个窗子的边框,如图所示,窗子是由一个矩形ABCD和以AD为直径的半圆组成,窗子的边框不包括矩形的AD边,设半圆的半径为OA=r(米),窗子的透光面积为S(平方米).
设计人员要用10米长的材料(材料的宽度不计)建造一个窗子的边框,如图所示,窗子是由一个矩形ABCD和以AD为直径的半圆组成,窗子的边框不包括矩形的AD边,设半圆的半径为OA=r(米),窗子的透光面积为S(平方米).分析 (1)设半圆的半径为OA=r(米),可得矩形的宽为2r,半圆的弧长为πr,可得矩形的高为$\frac{1}{2}$(10-2r-πr),运用半圆的面积和矩形的面积,即可所求透光面积S的解析式,由二次函数的最值求法,即可得到所求r;
(2)由r=1,分别求出窗子的半圆部分的造价和窗子的矩形部分的造价,求和,即可判断是否够用.
解答 解:(1) 设半圆的半径为OA=r(米),
设半圆的半径为OA=r(米),
可得矩形的宽为2r,半圆的弧长为πr,
可得矩形的高为$\frac{1}{2}$(10-2r-πr),
窗子的透光面积为S=$\frac{1}{2}$πr2+$\frac{1}{2}$(10-2r-πr)•2r
=(-2-$\frac{1}{2}$π)r2+10r,(0<r<$\frac{10}{2+π}$),
当r=-$\frac{10}{2(-2-\frac{1}{2}π)}$=$\frac{10}{4+π}$(米),S有最大值;
(2)由题意可得r=1时,窗子的半圆部分的造价为$\frac{1}{2}$π•12•300=150π(元),
窗子的矩形部分的造价为2•$\frac{1}{2}$(10-2-π)•100=800-100π(元),
可得总造价为150π+800-100π=800+50π>900,
则r=1时,900元的造价不够用.
点评 本题考查函数在实际问题中的运用,考查二次函数的最值的求法,注意运用二次函数的性质,同时考查化简整理的运算能力,属于中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x=\frac{π}{6}$ | B. | $x=\frac{π}{3}$ | C. | $x=\frac{5π}{12}$ | D. | $x=\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
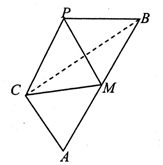 已知△ABC中,∠C=90°,tanA=$\sqrt{2}$,M为AB的中点,现将△ACM沿CM折成三棱锥P-CBM,当二面角P-CM-B大小为60°时,$\frac{AB}{PB}$=$\sqrt{3}$.
已知△ABC中,∠C=90°,tanA=$\sqrt{2}$,M为AB的中点,现将△ACM沿CM折成三棱锥P-CBM,当二面角P-CM-B大小为60°时,$\frac{AB}{PB}$=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | -1 | D. | 2018 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
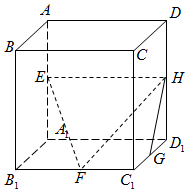 如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱AA1,B1C1,C1D1,DD1的中点,则GH与平面EFH所成角的余弦值为$\frac{3\sqrt{10}}{10}$.
如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱AA1,B1C1,C1D1,DD1的中点,则GH与平面EFH所成角的余弦值为$\frac{3\sqrt{10}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com