
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源:2015-2016学年四川省高二上学期期中考数学试卷(解析版) 题型:选择题
某加工厂用某原料由车间加工出 产品,由乙车间加工出 产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克 产品,每千克 产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克 产品,每千克 产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,甲、乙两车间每天获利最大的生产计划为( )
A.甲车间加工原料10箱,乙车间加工原料60箱
B.甲车间加工原料15箱,乙车间加工原料55箱
C.甲车间加工原料18箱,乙车间加工原料50箱
D.甲车间加工原料40箱,乙车间加工原料30箱
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}$ | B. | $4\sqrt{2}$ | C. | $2\sqrt{6}$ | D. | $2\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
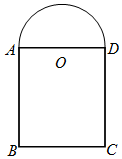 设计人员要用10米长的材料(材料的宽度不计)建造一个窗子的边框,如图所示,窗子是由一个矩形ABCD和以AD为直径的半圆组成,窗子的边框不包括矩形的AD边,设半圆的半径为OA=r(米),窗子的透光面积为S(平方米).
设计人员要用10米长的材料(材料的宽度不计)建造一个窗子的边框,如图所示,窗子是由一个矩形ABCD和以AD为直径的半圆组成,窗子的边框不包括矩形的AD边,设半圆的半径为OA=r(米),窗子的透光面积为S(平方米).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com