
| A. | $4\sqrt{3}$ | B. | $4\sqrt{2}$ | C. | $2\sqrt{6}$ | D. | $2\sqrt{5}$ |
分析 根据三角形内角和定理和正弦定理,利用三角函数的恒等变换,求得A、B、C的关系,再利用正弦定理计算a+b的值.
解答 解:△ABC中,bsinA+acos(B+C)=0,
∴bsinA-acosA=0,
由正弦定理得sinBsinA-sinAcosA=0,
又A∈(0,π),∴sinA≠0,
∴sinB-cosA=0,即cosA=sinB;
∴cosA=sin($\frac{π}{2}$+A)=sinB,
∴$\frac{π}{2}$+A+B=π,即C=A+B=$\frac{π}{2}$;
或B=$\frac{π}{2}$+A,即B-A=$\frac{π}{2}$;
又∵sinC=$\frac{3}{5}$,∴B-A=$\frac{π}{2}$,
∴cosC=sin($\frac{π}{2}$-C)=sin2A=2sinAcosA=$\frac{4}{5}$,
∴1+2sinAcosA=(sinA+cosA)2=$\frac{9}{5}$,
解得sinA+cosA=$\frac{3\sqrt{5}}{5}$;
∴a+b=$\frac{c}{sinC}$(sinA+sinB)=$\frac{10}{3}$(sinA+cosA)=$\frac{10}{3}$×$\frac{3\sqrt{5}}{5}$=2$\sqrt{5}$.
故选:D.
点评 本题考查了三角恒等变换以及正弦定理与三角形内角和定理的应用问题,是综合题.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
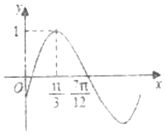 函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的图象如图所示,为了得到g(x)=Asinωx的图象,可以将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的图象如图所示,为了得到g(x)=Asinωx的图象,可以将f(x)的图象( )| A. | 向左平移$\frac{π}{12}$个单位长度 | B. | 向右平移$\frac{π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 第十届中国艺术节在山东济南胜利闭幕,山东省京剧院的京剧《瑞蚨祥》获得“第十四届文华奖--文华大奖”,评委给她的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91,现场做的9个分数的茎叶图后来有一个数据模糊,无法辨认,在图中以x表示:则7个剩余分数的方差为$\frac{36}{7}$.
第十届中国艺术节在山东济南胜利闭幕,山东省京剧院的京剧《瑞蚨祥》获得“第十四届文华奖--文华大奖”,评委给她的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91,现场做的9个分数的茎叶图后来有一个数据模糊,无法辨认,在图中以x表示:则7个剩余分数的方差为$\frac{36}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{1,\frac{5}{4}}]$ | B. | [-1,1] | C. | (-∞,1] | D. | $({-∞,\frac{5}{4}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com