
| A. | $x=\frac{π}{6}$ | B. | $x=\frac{π}{3}$ | C. | $x=\frac{5π}{12}$ | D. | $x=\frac{π}{3}$ |
分析 利用函数y=Asin(ωx+φ)的图象变换规律求得平移后f(x-$\frac{π}{12}$)的解析式,再利用正弦函数的图象的对称性,求得平移后得到的图象的一个对称轴.
解答 解:令$f(x)=sin({\frac{π}{6}-2x})=-sin({2x-\frac{π}{6}})$,将函数$y=sin({\frac{π}{6}-2x})$的图象向右平移$\frac{π}{12}$个单位后得到的图象对应的解析式为y=f(x-$\frac{π}{12}$),
则$f({x-\frac{π}{12}})=-sin[{2({x-\frac{π}{12}})-\frac{π}{6}}]=-sin({2x-\frac{π}{3}})$,由$2x-\frac{π}{3}=kπ+\frac{π}{2}(k∈Z)$,得其对称轴方程为:$x=\frac{kπ}{2}+\frac{5}{12}π(k∈Z)$,
当k=0时,$x=\frac{5}{12}π$,即为将函数$y=sin({\frac{π}{6}-2x})$的图象向右平移$\frac{π}{12}$个单位后所得的图象的一个对称轴,
故选:C.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:选择题
| A. | $\lim_{n→∞}{a_n}$和$\lim_{n→∞}{S_n}$都存在 | B. | $\lim_{n→∞}{a_n}$和$\lim_{n→∞}{S_n}$都不存在 | ||
| C. | $\lim_{n→∞}{a_n}$存在,$\lim_{n→∞}{S_n}$不存在 | D. | $\lim_{n→∞}{a_n}$不存在,$\lim_{n→∞}{S_n}$存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
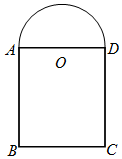 设计人员要用10米长的材料(材料的宽度不计)建造一个窗子的边框,如图所示,窗子是由一个矩形ABCD和以AD为直径的半圆组成,窗子的边框不包括矩形的AD边,设半圆的半径为OA=r(米),窗子的透光面积为S(平方米).
设计人员要用10米长的材料(材料的宽度不计)建造一个窗子的边框,如图所示,窗子是由一个矩形ABCD和以AD为直径的半圆组成,窗子的边框不包括矩形的AD边,设半圆的半径为OA=r(米),窗子的透光面积为S(平方米).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
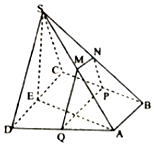 如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=CD=SD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD的中点,过M,N作平面MNPQ分别与交BC,AD于点P,Q.
如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=CD=SD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD的中点,过M,N作平面MNPQ分别与交BC,AD于点P,Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com