
| A. | 2 | B. | $\frac{1}{2}$ | C. | -1 | D. | 2018 |
分析 利用数列的递推关系式,逐步求解即可.
解答 解:数列{an}满足:a1=2,an+1=$\frac{{a}_{n}-1}{{a}_{n}}$,则a2=$\frac{2-1}{2}$=$\frac{1}{2}$,
a3=$\frac{\frac{1}{2}-1}{\frac{1}{2}}$=-1
a4=$\frac{-1-1}{-1}$=2
a5=$\frac{2-1}{2}$=$\frac{1}{2}$,
a6=$\frac{\frac{1}{2}-1}{\frac{1}{2}}$=-1.
a7=$\frac{-1-1}{-1}$=2.
故选:A.
点评 本题考查数列的递推关系式的应用,考查计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
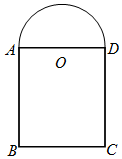 设计人员要用10米长的材料(材料的宽度不计)建造一个窗子的边框,如图所示,窗子是由一个矩形ABCD和以AD为直径的半圆组成,窗子的边框不包括矩形的AD边,设半圆的半径为OA=r(米),窗子的透光面积为S(平方米).
设计人员要用10米长的材料(材料的宽度不计)建造一个窗子的边框,如图所示,窗子是由一个矩形ABCD和以AD为直径的半圆组成,窗子的边框不包括矩形的AD边,设半圆的半径为OA=r(米),窗子的透光面积为S(平方米).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
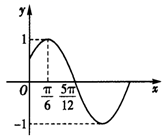
| A. | $f(x)=sin({2x-\frac{π}{6}})$(x∈R) | B. | $f(x)=sin({2x+\frac{π}{6}})$(x∈R) | C. | $f(x)=sin({2x-\frac{π}{3}})$(x∈R) | D. | $f(x)=sin({2x+\frac{π}{3}})$(x∈R) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com