
分析 根据定积分求得a的值,利用二项式定理,求得其通项公式,Tk+1=${C}_{18}^{k}$${x}^{\frac{54-5k}{6}}$,0≤k≤18,分别代入,当k=6,k=12,k=18,x幂指数是整数,则x的幂指数不是整数的项15项.
解答 解:$a=2\int_{-3}^3{({x+|x|})dx}$=2(${∫}_{-3}^{3}$xdx+${∫}_{-3}^{3}$丨x丨dx)=4${∫}_{0}^{3}$xdx=18,
${({\sqrt{x}-\frac{1}{{\root{3}{x}}}})^a}$=($\sqrt{x}$-$\frac{1}{\root{3}{x}}$)18,则Tk+1=${C}_{18}^{k}$($\sqrt{x}$)18-k($\frac{1}{\root{3}{x}}$)k,
=${C}_{18}^{k}$${x}^{\frac{54-5k}{6}}$,0≤k≤18,
则当k=0,k=6,k=12,k=18,x幂指数是整数,
∴x的幂指数不是整数的项共19-4=15,
故答案为:15.
点评 本题考查定积分的运算,考查二项式定理的应用,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | -1 | D. | 2018 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
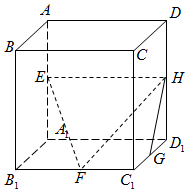 如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱AA1,B1C1,C1D1,DD1的中点,则GH与平面EFH所成角的余弦值为$\frac{3\sqrt{10}}{10}$.
如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱AA1,B1C1,C1D1,DD1的中点,则GH与平面EFH所成角的余弦值为$\frac{3\sqrt{10}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com