Question

10．已知函数f（x）=$\frac{a{x}^{2}+2x-1}{{e}^{2x}}$，g（x）=-2xln（1+$\frac{1}{x}$）-lnf（x）．
（Ⅰ）讨论函数f（x）的单调性；
（Ⅱ）当a=0时，函数g（x）在定义域内是否存在零点？如果存在，求出该零点；如果不存在，请说明理由．

Answer 1

分析 （Ⅰ）函数f（x）的定义域为R，f′（x）=$\frac{-2（ax+2）（x-1）}{{e}^{2x}}$，分①a=0，②a＞0，③a＜0讨论其单调性．
（Ⅱ）a=0时，函数g（x）=-2xln$\frac{x+1}{x}$-ln$\frac{2x-1}{{e}^{2x}}$=-2xln（x+1）+2xlnx-ln$\frac{2x-1}{{e}^{2x}}$（x＞$\frac{1}{2}$），函数g（x）在定义域内是否存在零点?函数G（x）=-2xln（x+1）+2xlnx与R（x）=ln$\frac{2x-1}{{e}^{2x}}$，（x＞$\frac{1}{2}$）是否有交点．分别讨论两函数的单调性，画出图象，结合图象求解．

解答 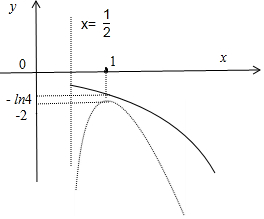解：（Ⅰ）函数f（x）的定义域为R，f′（x）=$\frac{（2ax+2）{e}^{2x}-2（a{x}^{2}+2x-1）{e}^{2x}}{{（e}^{2x}）^{2}}$=$\frac{2[-a{x}^{2}+（a-2）x+2]}{{e}^{2x}}$=$\frac{-2（ax+2）（x-1）}{{e}^{2x}}$
①a=0时，f（′（x）=2×$\frac{-2（x-1）}{{e}^{2x}}$，可得x∈（-∞，1）时，f′（x）＞0，x∈（1，+∞），f′（x）＜0，
此时f（x）在（-∞，1）递增，在（1，+∞）递减．
②a＞0时，令f′（x）=0，x=1或x=-$\frac{2}{a}$，可得x∈（-$\frac{2}{a}$，1）时，f′（x）＞0，x∈（1，+∞）∪（-∞，-$\frac{2}{a}$），f′（x）＜0，
此时f（x）在（-$\frac{2}{a}$，1）递增，在（-$∞，-\frac{2}{a}$），（1，+∞）递减．
③a＜0时，令f′（x）=0，x=1或x=-$\frac{2}{a}$，
0＞a＞-2时，-$\frac{2}{a}＞1＞0$，此时f（x）在（-∞，1），（-$\frac{2}{a}，+∞$）递增，在（1，-$\frac{2}{a}$）递减．
a＜-2时，1$＞-\frac{2}{a}＞0$，此时f（x）在（-∞，-$\frac{2}{a}$），（1，+∞）递增，在（-$\frac{2}{a}$，1）递减．
a=-2时．此时f（x）在（-∞，+∞）递增．
（Ⅱ）当a=0时，函数g（x）在定义域内不存在零点，理由如下：
a=0时，函数g（x）=-2xln$\frac{x+1}{x}$-ln$\frac{2x-1}{{e}^{2x}}$=-2xln（x+1）+2xlnx-ln$\frac{2x-1}{{e}^{2x}}$，（x＞$\frac{1}{2}$）．
函数g（x）在定义域内是否存在零点?函数G（x）=-2xln（x+1）+2xlnx与R（x）=ln$\frac{2x-1}{{e}^{2x}}$，（x＞$\frac{1}{2}$）是否有交点．
       一方面：由（Ⅰ）知y=$\frac{2x-1}{{e}^{2x}}$在（-∞，1）递增，在（1，+∞）递减，可得R（x）=ln$\frac{2x-1}{{e}^{2x}}$，（x＞$\frac{1}{2}$）在 （$\frac{1}{2}$，1）递增，在（1，+∞）递减
且x→$\frac{1}{2}$，R（x）→-∞，x→+∞，R（x）→-∞，R（1）=-2＜0
      另一方面：G′（x）=2[lnx-ln（x+1）+$\frac{1}{x+1}$]，G″（x）=2[$\frac{1}{x（x+1）}$-$\frac{1}{（x+1）^{2}}$]＞0在（$\frac{1}{2}，+∞$）恒成立．
∴G′（x）在（$\frac{1}{2}，+∞$）递增，而G′（$\frac{1}{2}$）=2（-ln3+$\frac{2}{3}$）＜0，x→+∞时，G（x）→0，∴G′（x）＜0．
∴函数G（x）在（$\frac{1}{2}，+∞$）递减，G（$\frac{1}{2}$）=-ln3＜0．
由此可以在同一坐标系画出两函数，如下：
结合图象可得，当a=0时，函数g（x）在定义域内不存在零点

点评 本题考查了利用导数求函数单调性，函数极值点，考查了分类讨论、数形结合思想，属于难题．