
���� ��I����N��x��y�������P�����꣬����$\overrightarrow{MP}•\overrightarrow{PN}$=0�з��̻��ɣ�
��II��������������Ԫ�����ø���ϵ���Ĺ�ϵ���ҳ���ʽ����|AB|��AB���е�F�����꣬��F��x��ľ���d��$\frac{1}{2}$|AB|������б�ʽ����0�в���ʽ����k�ķ�Χ��
��� �⣺��I����N��x��y������$\overrightarrow{PN}=\frac{1}{2}\overrightarrow{NQ}$����P��0��$\frac{3y}{2}$����
��$\overrightarrow{MP}$=��3��$\frac{3y}{2}$����$\overrightarrow{PN}$=��x��-$\frac{y}{2}$����
��$\overrightarrow{MP}•\overrightarrow{PN}$=3x-$\frac{3{y}^{2}}{4}$=0����y2=4x��
���N�Ĺ켣C�ķ�����y2=4x��
��II��ֱ��l�ķ���Ϊy=k��x+$\frac{1}{2}$����k��0����
����������$\left\{\begin{array}{l}{y=k��x+\frac{1}{2}��}\\{{y}^{2}=4x}\end{array}\right.$����Ԫ��ky2-4y+2k=0��
���=16-8k2��0�����-$\sqrt{2}$��k��0��0��k��$\sqrt{2}$��
��A��x1��y1����B��x2��y2������y1+y2=$\frac{4}{k}$��y1y2=2��
��|AB|=$\sqrt{1+\frac{1}{{k}^{2}}}$$\sqrt{��{y}_{1}+{y}_{2}��^{2}-4{y}_{1}{y}_{2}}$=$\frac{\sqrt{1+{k}^{2}}\sqrt{16-8{k}^{2}}}{{k}^{2}}$��
��AB���е�ΪF����x1+x2=$\frac{{{y}_{1}}^{2}+{{y}_{2}}^{2}}{4}$=$\frac{4}{{k}^{2}}$-1����F��$\frac{2}{{k}^{2}}$-$\frac{1}{2}$��$\frac{2}{k}$����
��x���ϴ���һ��E��x0��0����ʹ�á�AEB���Ե�EΪֱ�Ƕ����ֱ�������Σ�
��F��x��ľ���d��|EF|=$\frac{1}{2}$|AB|��
��$|\frac{2}{k}|$��$\frac{1}{2}$•$\frac{\sqrt{1+{k}^{2}}\sqrt{16-8{k}^{2}}}{{k}^{2}}$�������k4+k2-2��0�����0��k2��1��
��-$\sqrt{2}$��k��0��0��k��$\sqrt{2}$��
��ֱ��l��б��k�ķ�Χ��[-1��0���ȣ�0��1]��
���� ���⿼���˹켣���̵���⣬ֱ���������ߵ�λ�ù�ϵ�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\lim_{n����}{a_n}$��$\lim_{n����}{S_n}$������ | B�� | $\lim_{n����}{a_n}$��$\lim_{n����}{S_n}$�������� | ||
| C�� | $\lim_{n����}{a_n}$���ڣ�$\lim_{n����}{S_n}$������ | D�� | $\lim_{n����}{a_n}$�����ڣ�$\lim_{n����}{S_n}$���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{1}{6}$ | D�� | $\frac{3}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 4 | C�� | 6 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | c��b��a | C�� | a��c��b | D�� | c��a��b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
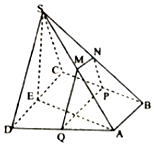 ��ͼ������S-ABCD�У�����ABCDΪֱ�����Σ�AB��CD��BC��CD��ƽ��SCD��ƽ��ABCD��SC=CD=SD=AD=2AB=2��M��N�ֱ�ΪSA��SB���е㣬EΪCD���е㣬��M��N��ƽ��MNPQ�ֱ��뽻BC��AD�ڵ�P��Q��
��ͼ������S-ABCD�У�����ABCDΪֱ�����Σ�AB��CD��BC��CD��ƽ��SCD��ƽ��ABCD��SC=CD=SD=AD=2AB=2��M��N�ֱ�ΪSA��SB���е㣬EΪCD���е㣬��M��N��ƽ��MNPQ�ֱ��뽻BC��AD�ڵ�P��Q���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
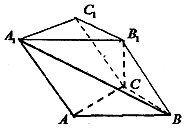 ��ͼ��б������ABC-A1B1C1�У�����AA1B1BΪ���Σ������ABC�ǵ���ֱ�������Σ���BAC=90�㣬A1B��B1C��
��ͼ��б������ABC-A1B1C1�У�����AA1B1BΪ���Σ������ABC�ǵ���ֱ�������Σ���BAC=90�㣬A1B��B1C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com