
| A. | a>b>c | B. | c>b>a | C. | a>c>b | D. | c>a>b |
分析 根据题意,构造函数h(x)=xf(x),则a=h(20.6),b=h(ln2),c=(${{{log}_2}\frac{1}{8}}$)•f(${{{log}_2}\frac{1}{8}}$)=h(-3),分析可得h(x)为奇函数且在(-∞,0)上为减函数,进而分析可得h(x)在(0,+∞)上为减函数,分析有${{{log}_2}\frac{1}{8}}$<0<ln2<1<20.6,结合函数的单调性分析可得答案.
解答 解:根据题意,令h(x)=xf(x),
h(-x)=(-x)f(-x)=-xf(x)=-h(x),则h(x)为奇函数;
当x∈(-∞,0)时,h′(x)=f(x)+xf'(x)<0,则h(x)在(-∞,0)上为减函数,
又由函数h(x)为奇函数,则h(x)在(0,+∞)上为减函数,
a=(20.6)•f(20.6)=h(20.6),b=(ln2)•f(ln2)=h(ln2),c=(${{{log}_2}\frac{1}{8}}$)•f(${{{log}_2}\frac{1}{8}}$)=h(${{{log}_2}\frac{1}{8}}$)=h(-3),
因为${{{log}_2}\frac{1}{8}}$<0<ln2<1<20.6,
则有c>a>b;
故选:D.
点评 本题考查函数奇偶性与单调性的综合应用,关键是构造函数h(x)=xf(x),并分析h(x)的奇偶性与单调性.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | log23<log35 | B. | ?x∈(-∞,0),ex>x+1 | ||
| C. | ${log_{\frac{1}{2}}}3<{(\frac{1}{2})^3}<{3^{\frac{1}{2}}}$ | D. | ?x>0,x>sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
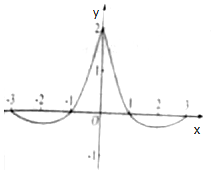 已知函数f(x)=$\frac{{cos({ωx+φ})}}{{a•{e^{|x|}}}}$(ω>0,|φ|<$\frac{π}{2}$,a∈R)在区间[-3,3]上的图象如图所示,则$\frac{ω}{a}$可取( )
已知函数f(x)=$\frac{{cos({ωx+φ})}}{{a•{e^{|x|}}}}$(ω>0,|φ|<$\frac{π}{2}$,a∈R)在区间[-3,3]上的图象如图所示,则$\frac{ω}{a}$可取( )| A. | 4π | B. | 2π | C. | π | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com