
分析 由$\frac{y(z-x)}{x(y-z)}$=$\frac{z(y-x)}{y(z-x)}$,得$\frac{yz-yx}{xy-xz}$=1+$\frac{xy-xz}{yz-xy}$,由此能求出公比q.
解答 解:∵三个非零实数:x(y-z)、y(z-x)、z(y-x)成等比数列,
∴$\frac{y(z-x)}{x(y-z)}$=$\frac{z(y-x)}{y(z-x)}$,即$\frac{yz-yx}{xy-xz}$=$\frac{yz-xz}{yz-xy}$,
又$\frac{yz-xz}{yz-xy}$=$\frac{yz-xy+xy-xz}{yz-xy}$=1+$\frac{xy-xz}{yz-xy}$,
$\frac{yz-yx}{xy-xz}$=1+$\frac{xy-xz}{yz-xy}$,
设$\frac{yz-yx}{xy-xz}$=q,则q=1+$\frac{1}{q}$,
解得:q=$\frac{1±\sqrt{5}}{2}$.
故答案为:$\frac{{1±\sqrt{5}}}{2}$.
点评 本题考查等比数列中项数的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>b>a | C. | a>c>b | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
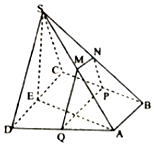 如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=CD=SD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD的中点,过M,N作平面MNPQ分别与交BC,AD于点P,Q.
如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=CD=SD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD的中点,过M,N作平面MNPQ分别与交BC,AD于点P,Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
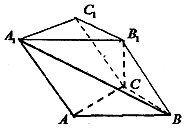 如图,斜三棱柱ABC-A1B1C1中,侧面AA1B1B为菱形,底面△ABC是等腰直角三角形,∠BAC=90°,A1B⊥B1C.
如图,斜三棱柱ABC-A1B1C1中,侧面AA1B1B为菱形,底面△ABC是等腰直角三角形,∠BAC=90°,A1B⊥B1C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{5}{4}$ | C. | $\frac{7}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com