
分析 (1)当$a=\frac{1}{2}$时,f'(x)=ex-1+xex-x=(ex-1)(x+1),由此利用导数性质能求出函数f(x)的单调区间.
(2)若f(x)在(-1,0)内无极值,则f(x)在(-1,0)上单调,又f'(x)=(x+1)ex-2ax-1,由此利用分类讨论思想及导数的性质能求出a的取值范围.
(3)用数学归纳法能证明${e^x}>1+\frac{x}{1!}+\frac{x^2}{2!}+…+\frac{x^n}{n!}$.
解答 (本小题满分12分)
解:(1)当$a=\frac{1}{2}$时,$f(x)=x({e^x}-1)-\frac{1}{2}{x^2}$
所以f'(x)=ex-1+xex-x=(ex-1)(x+1)
当x∈(-∞,-1)时,f'(x)>0;当x∈(-1,0)时,f'(x)<0;
当x∈(0,+∞)时,f'(x)>0
故f(x)在(-∞,-1),(0,+∞)单调递增,在(-1,0)单调递减. …(4分)
(2)若f(x)在(-1,0)内无极值,则f(x)在(-1,0)上单调,
又f'(x)=(x+1)ex-2ax-1
①若f(x)在(-1,0)上递减,则f'(x)≤0,对x∈(-1,0)恒成立,
于是有$2a≤\frac{{(x+1){e^x}-1}}{x}={e^x}+\frac{{{e^x}-1}}{x}$,令$g(x)={e^x}+\frac{{{e^x}-1}}{x},h(x)=\frac{{{e^x}-1}}{x}$,
下面证明h(x)在(-∞,0)上单调递增:$h'(x)=\frac{{(x-1){e^x}+1}}{x^2}$,令r(x)=(r-1)ex+1,则r'(x)=(x-1)ex+ex=xex
当x<0时,r'(x)<0,r(x)单调递减,r(x)>r(0)=0,h'(x)>0h(x)在(-∞,0)单调递增.
当x∈(-1,0)时,由g(x)=ex+h(x)是增函数,得g(x)>g(-1)=1.
由2a≤g(x),得$2a≤1,a≤\frac{1}{2}$;
②若f(x)在(-1,0)上单调递增,则f'(x)≥0,对x∈(-1,0)恒成立,
于是2a≥g(x),当x∈(-1,0)时,由ex>x+1得$h(x)=\frac{{{e^x}-1}}{x}<1$,
从而增函数g(x)=ex+h(x)<2,这样2a>2,a>1.综上得$a∈({-∞,\frac{1}{2}}]∪[{1,+∞})$.…(8分)
证明:(3)用数学归纳法证明 ①当n=1时,ex>x+1,不等式成立;
②假设n=k时不等式成立,即${e^x}>1+\frac{x}{1!}+\frac{x^2}{2!}+…+\frac{x^k}{k!}$,
当n=k+1时,令$ϕ(x)={e^x}-(1+\frac{x}{1!}+\frac{x^2}{2!}+…+\frac{x^k}{k!}+\frac{{{x^{k+1}}}}{(k+1)!}),x>0$
显然ϕ(0)=0,由归纳假设,$ϕ'(x)={e^x}-(1+\frac{x}{1!}+\frac{x^2}{2!}+…+\frac{x^k}{k!})>0$对x>0成立,
所以ϕ(x)在(0,+∞)上单调递增,当x>0时,ϕ(x)>ϕ(0)=0,即当n=k+1
时,不等式也成立.
综合①②n∈N+,x>0时,${e^x}>1+\frac{x}{1!}+\frac{x^2}{2!}+…+\frac{x^n}{n!}$. …(12分)
点评 本题考查导数的几何意义、导数性质、构造法、函数性质、不等式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、分类与整合思想,考查创新意识、应用意识,是中档题.


科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
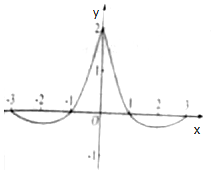 已知函数f(x)=$\frac{{cos({ωx+φ})}}{{a•{e^{|x|}}}}$(ω>0,|φ|<$\frac{π}{2}$,a∈R)在区间[-3,3]上的图象如图所示,则$\frac{ω}{a}$可取( )
已知函数f(x)=$\frac{{cos({ωx+φ})}}{{a•{e^{|x|}}}}$(ω>0,|φ|<$\frac{π}{2}$,a∈R)在区间[-3,3]上的图象如图所示,则$\frac{ω}{a}$可取( )| A. | 4π | B. | 2π | C. | π | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com