
分析 根据三角形的有关计算可得OA=2,OB=4,OC=3,如图以OB,OC所在的直线分别为x轴,y轴建立直角坐标系,设P(x,y),根据向量的坐标运算即可求出P的坐标,结合图象可得最值得问值,根据点到直线的距离公式计算即可
解答  解:在△ABC中过点C作OD⊥AB交AB于点O,则AC2-OA2=BC2-OB2,
解:在△ABC中过点C作OD⊥AB交AB于点O,则AC2-OA2=BC2-OB2,
即OB2-OA2=(OB-OA)(OB+OA)=12,
又OA+OB=6,
解得OA=2,OB=4,
所以OC=3,
如图以OB,OC所在的直线分别为x轴,y轴建立直角坐标系,
所以A=(-2,0),B(4,0),C(0,3),
设P(x,y),
∵$3\overrightarrow{AP}=\overrightarrow{PB}+2\overrightarrow{PC}$,
∴3($\overrightarrow{OP}$-$\overrightarrow{OA}$)=$\overrightarrow{OB}$-$\overrightarrow{OP}$+2($\overrightarrow{OC}$-$\overrightarrow{OP}$),
∴$\overrightarrow{OP}$=$\frac{1}{6}$(3$\overrightarrow{OA}$+$\overrightarrow{OB}$+2$\overrightarrow{OC}$)=$\frac{1}{6}$(-2,6)=(-$\frac{1}{3}$,1),
即P点的坐标为(-$\frac{1}{3}$,1),
易知P到△ABC中BC边的距离最大,
又直线BC的方程为3x+4y-12=0,
∴点P到△ABC三边的距离的最大值为$\frac{|-1+4-12|}{\sqrt{{3}^{2}+{4}^{2}}}$=$\frac{9}{5}$,
故答案为:$\frac{9}{5}$
点评 本题考查了向量的坐标运算和点到直线的距离公式,属于中档题


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015-2016学年四川省高二上学期期中考数学试卷(解析版) 题型:选择题
若直线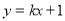 与圆
与圆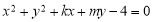 交于
交于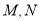 两点,且
两点,且 关于直线
关于直线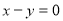 对称,动点P
对称,动点P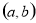 在不等式组
在不等式组 表示的平面区域内部及边界上运动,则
表示的平面区域内部及边界上运动,则 的取值范围是( )
的取值范围是( )
A.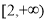 B.
B.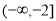
C. D.
D.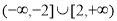
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
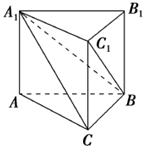 《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1千多年.在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖臑指四个面均为直角三角形的四面体.如图,在堑堵ABC-A1B1C1中,AC⊥BC.
《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1千多年.在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖臑指四个面均为直角三角形的四面体.如图,在堑堵ABC-A1B1C1中,AC⊥BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>c>a | C. | a>c>b | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{7}{3}$ | D. | $\frac{9}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com