
分析 (1)利用同角三角函数的基本关系,以及三角函数在各个象限中的符号,求得要求式子的值.
(2)利用同角三角函数的基本关系,求得要求式子的值.
解答 解:(1)∵函数f(x)=$\sqrt{\frac{1+sinx}{1-sinx}}$-$\sqrt{\frac{1-sinx}{1+sinx}}$,且f(α)=1,α为第二象限角.
∴$\sqrt{\frac{1+sinα}{1-sinα}}$-$\sqrt{\frac{1-sinα}{1+sinα}}$=|$\frac{1+sinα}{cosα}$|-|$\frac{1-sinα}{cosα}$|=-$\frac{1+sinα}{cosα}$-$\frac{sinα-1}{cosα}$=-2tanα=1,
∴tanα=-$\frac{1}{2}$.
(2)sinαcosα+5cos2α=$\frac{sinαcosα+{5cos}^{2}α}{{sin}^{2}α{+cos}^{2}α}$=$\frac{tanα+5}{{tan}^{2}α+1}$=$\frac{-\frac{1}{2}+5}{\frac{1}{4}+1}$=$\frac{18}{5}$.
点评 本题主要考查同角三角函数的基本关系,以及三角函数在各个象限中的符号,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:解答题
已知直线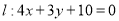 ,半径为
,半径为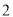 的圆
的圆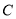 与
与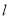 相切,圆心
相切,圆心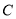 在
在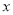 轴上且在直线
轴上且在直线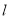 的右上方.
的右上方.
(1)求圆的方程;
(2)若直线过点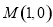 且与圆
且与圆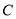 交于
交于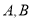 两点(
两点(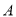 在
在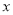 轴上方,B在
轴上方,B在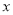 轴下方),问在
轴下方),问在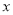 轴正半轴上是否存在定点
轴正半轴上是否存在定点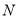 ,使得
,使得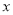 轴平分
轴平分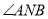 ?若存在,请求出点
?若存在,请求出点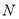 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 组号 | 分组 | 频数 |
| 1 | [53,61) | 5 |
| 2 | [61,69) | 14 |
| 3 | [69,77) | 25 |
| 4 | [77,85) | 11 |
| 5 | [85,93) | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小正周期是π | B. | 区间[0,2]上的增函数 | ||
| C. | 图象关于点(kπ,0)(k∈Z)对称 | D. | 周期函数且图象有无数条对称轴 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com