
分析 (Ⅰ)求解导数得出:h(x)=xex,(-∞,-1)上单调递减,(-1,+∞)单调递增,x=-1时h(x)去极小值.
(Ⅱ)当m=0时,记F(x)=f(x)-g(x)=ex-ax-b,F(x)在(-∞,ln2)上单调递减,在(ln2,+∞)上单调递增,F(x)的最小值为F(ln2)=2-2ln2-b,根据函数性质得出:2-2ln2-b<0,F(-1)≥0,F(2)≥0.
解答 解:(Ⅰ)∵函数f(x)=ex,函数h(x)=xf(x),
∴h(x)=xex,∴h′(x)=ex+xex,
∵h′(x)=ex+xex=0,x=-1,
h′(x)=ex+xex>0,x>-1,
h′(x)=ex+xex<0,x<-1,
∴h(x)=xex,(-∞,-1)上单调递减,(-1,+∞)单调递增,x=-1时h(x)取极小值,
∵当a=1,b=0时g(x)=mx2+ax+b=mx2+x,若函数h(x)与g(x)具有相同的单调区间,
∴-$\frac{1}{2m}$=-1,m=$\frac{1}{2}$;
(Ⅱ)当m=0,a=2时,F(x)=ex-2x-b,
∴F′(x)=ex-2,
∵F′(x)=ex-2=0,x=ln2,
F′(x)=ex-2>0,x>ln2
F′(x)=ex-2<0,x<ln2,
∴F(x)在(-∞,ln2)上单调递减,在(ln2,+∞)上单调递增,
F(x)的最小值为F(ln2)=2-2ln2-b,
∵函数F(x)在[-1,2]上存在两个不同的零点,
∴2-2ln2-b<0,F(-1)≥0,F(2)≥0,
解得出:b>2-2ln2,b≤$\frac{1}{e}$+2,b≤e2-4,
即2-2ln2<b≤$\frac{1}{e}$+2.
点评 本题考查了函数思想的运用,导数在求解单调性,最值中的应用,知识比较多,难度较大.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
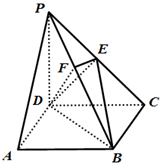 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,E是PC的中点,作EF⊥PB交PB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1≤x≤2} | B. | {x|x≥1} | C. | {x|1<x≤2} | D. | {x|2≤x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com