
分析 (1)由曲线C的极坐标方程能求出曲线C的直角坐标方程,求出点P的直角坐标为$({0,\sqrt{3}})$,直线l的倾斜角为135°,由此能求出直线l的参数方程.
(2)将$\left\{\begin{array}{l}x=-\frac{{\sqrt{2}}}{2}t\\ y=\sqrt{3}+\frac{{\sqrt{2}}}{2}t\end{array}\right.(t$为参数)代入${({x-1})^2}+{({y-\sqrt{3}})^2}=4$,得${t^2}+\sqrt{2}t-3=0$,设A,B对应参数分别为t1t2,根据直线参数方程t的几何意义,能求出结果.
解答 解:(1)由曲线C的极坐标方程$ρ=4cos({θ-\frac{π}{3}})$可得$ρ=2cosθ+2\sqrt{3}sinθ$,
即${ρ^2}=2ρcosθ+2\sqrt{3}ρsinθ$,
因此曲线C的直角坐标方程为${x^2}+{y^2}-2x-2\sqrt{3}y=0$,
即${({x-1})^2}+{({y-\sqrt{3}})^2}=4$,点P的直角坐标为$({0,\sqrt{3}})$,
直线l的倾斜角为135°,
所以直线l的参数方程为$\left\{\begin{array}{l}x=-\frac{{\sqrt{2}}}{2}t\\ y=\sqrt{3}+\frac{{\sqrt{2}}}{2}t\end{array}\right.(t$为参数).
(2)将$\left\{\begin{array}{l}x=-\frac{{\sqrt{2}}}{2}t\\ y=\sqrt{3}+\frac{{\sqrt{2}}}{2}t\end{array}\right.(t$为参数)代入${({x-1})^2}+{({y-\sqrt{3}})^2}=4$,
得${t^2}+\sqrt{2}t-3=0$,设A,B对应参数分别为t1t2,
有${t_1}+{t_2}=\sqrt{2},{t_1}{t_2}=-3$,根据直线参数方程 t的几何意义,得:
$\frac{{|{PA}|}}{{|{PB}|}}+\frac{{|{PB}|}}{{|{PA}|}}=\frac{{{{|{PA}|}^2}+{{|{PB}|}^2}}}{{|{PA}|•|{PB}|}}=\frac{{{t_1}^2+{t_2}^2}}{{|{{t_1}{t_2}}|}}=\frac{{{{({{t_1}+{t_2}})}^2}-2{t_1}{t_2}}}{{|{{t_1}{t_2}}|}}=\frac{8}{3}$.
点评 本题考查极坐标方程、参数方程、直角坐标方程等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、化归与转化思想,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7200种 | B. | 1440种 | C. | 1200种 | D. | 2880种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{4\sqrt{3}-3}}{10}$ | B. | $\frac{{4\sqrt{3}+3}}{10}$ | C. | $\frac{{3-4\sqrt{3}}}{10}$ | D. | $\frac{{4\sqrt{3}+3}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
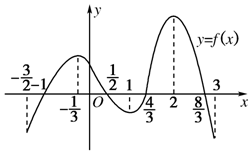 函数y=f(x)在定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
函数y=f(x)在定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )| A. | $[{-\frac{1}{3},1}]∪[2,3]$ | B. | $[{-1,\frac{1}{2}}]∪[{\frac{4}{3},\frac{8}{3}}]$ | ||
| C. | $[{-\frac{3}{2},\frac{1}{2}}]∪[1,2)$ | D. | $[{-\frac{3}{2},-\frac{1}{3}}]∪[{\frac{1}{2},\frac{4}{3}}]∪[{\frac{4}{3},3}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com