
分析 (Ⅰ)利用三角函数的诱导公式化简即可;
(Ⅱ)把特殊角的三角函数值代入计算即可.
解答 解:(Ⅰ)$\frac{{{{sin}^2}(α-\frac{π}{2})}}{{cos(α-3π)+sin(\frac{3π}{2}+α)}}$=$\frac{co{s}^{2}α}{-cosα-cosα}=-\frac{1}{2}cosα$;
(Ⅱ)sin30°cos60°+tan45°cos90°-sin180°cos270°=$\frac{1}{2}×\frac{1}{2}+0-0=\frac{1}{4}$.
点评 本题考查了三角函数的诱导公式,考查了特殊角的三角函数值,是基础题.


科目:高中数学 来源:2016-2017学年河南省新乡市高二上学期入学考数学卷(解析版) 题型:选择题
对于函数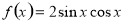 ,下列选项中正确的是
,下列选项中正确的是
A.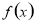 在
在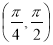 上是递增的
上是递增的
B.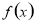 的图像关于原点对称
的图像关于原点对称
C.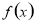 的最小正周期为
的最小正周期为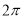
D.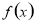 的最大值为2
的最大值为2
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
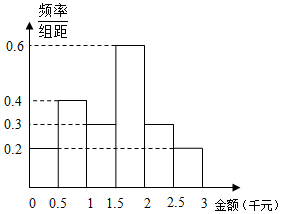 某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:
某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:| 网购达人 | 非网购达人 | 合计 | |
| 男性 | 30 | ||
| 女性 | 12 | 30 | |
| 合计 | 60 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | $[{\frac{{\sqrt{3}}}{2},1}]$ | C. | $[{\frac{1}{2},\frac{{\sqrt{3}}}{2}}]$ | D. | $[{\frac{1}{2},1}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com