
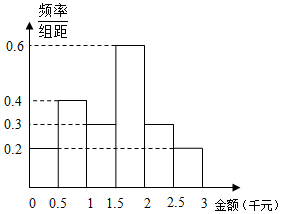
 ij����Ӫ������Ϊ��ͳ��ij������2016��12��12�յ�����������Ӹ��е�����������Ĺ˿�������������Ů��30�ˣ�ͳ�����������õ�����Ƶ�ʷֲ�ֱ��ͼ��
ij����Ӫ������Ϊ��ͳ��ij������2016��12��12�յ�����������Ӹ��е�����������Ĺ˿�������������Ů��30�ˣ�ͳ�����������õ�����Ƶ�ʷֲ�ֱ��ͼ��| �������� | ���������� | �ϼ� | |
| ���� | 30 | ||
| �� | 12 | 30 | |
| �ϼ� | 60 |
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���� ���������⣬��д������������K2�������ٽ�ֵ�ó����ۣ�
�� II������֪�εĿ���ȡֵ�������Ӧ�ĸ���ֵ��д���εķֲ��У�������ѧ����ֵ��
��� �⣺���������⣬��д���������£�
| �������� | ���������� | �ϼ� | |
| ���� | 3 | 27 | 30 |
| �� | 12 | 18 | 30 |
| �ϼ� | 15 | 45 | 60 |
| �� | 0 | 1 | 2 | 3 |
| P | $\frac{21}{55}$ | $\frac{27}{55}$ | $\frac{27}{220}$ | $\frac{1}{220}$ |
���� ���⿼���˶����Լ�������ɢ����������ķֲ��к���ѧ�����ļ������⣬���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꽭��ʡ��һ��ѧ�ڵ�һ���¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
��֪���� ��
��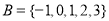 ����
����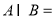 �� ��
�� ��
A��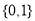 B��
B��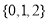 C��
C��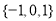 D��
D��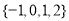
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ��ӱ�ʡ�߶����ϵ�һ���¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
����S��ABC��������ͼ�е�����ͼ�Ͳ���ͼ��ͼ��ʾ������SB�ij�Ϊ�� ��
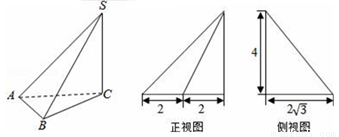
A��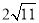 B��
B��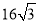 C��
C��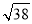 D��
D��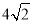
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | 3 | C�� | $\sqrt{5}$ | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{5}{8}$ | B�� | $\frac{5\sqrt{3}}{2}$ | C�� | 10$\sqrt{3}$ | D�� | $\frac{35}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-6��2�� | B�� | ��6��-2�� | C�� | ��-2��0�� | D�� | ��2��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com