
分析 作出此直二面角的图象,由图形中所给的位置关系对命题逐一判断,即可得出正确结论.
解答 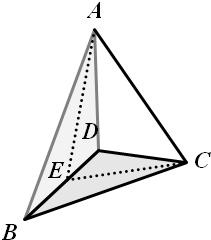 解:作出如图的图象,其中A-BD-C=90°,E是BD的中点,可以证明出∠AED=90°即为此直二面角的平面角
解:作出如图的图象,其中A-BD-C=90°,E是BD的中点,可以证明出∠AED=90°即为此直二面角的平面角
对于命题①,由于BD⊥面AEC,故AC⊥BD,此命题正确;
对于命题②,在等腰直角三角形AEC中可以解出AC等于正方形的边长,故△ACD是等边三角形,此命题正确;
对于命题③AB与平面BCD所成的线面角的平面角是∠ABE=45°,故AB与平面BCD成60°的角不正确;
综上知①②是正确的.
故答案为:①②.
点评 本题考查与二面角有关立体几何中线线之间的角的求法,线面之间的角的求法,以及线线之间位置关系的证明方法.综合性较强,对空间立体感要求较高.


科目:高中数学 来源: 题型:解答题
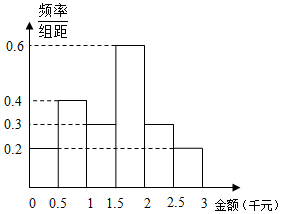 某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:
某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:| 网购达人 | 非网购达人 | 合计 | |
| 男性 | 30 | ||
| 女性 | 12 | 30 | |
| 合计 | 60 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 60° | C. | 150° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com