
分析 求出函数的导数,得到函数的单调区间,从而求出函数的极值以及端点值,根据函数的零点求出a的范围即可.
解答 解:若函数f(x)=x3-3x+5-a,
则f′(x)=3x2-3=3(x-1)(x+1),
令f′(x)>0,解得:x>1或x<-1,
令f′(x)<0,解得:-1<x<1,
故f(x)在(-3,-1)递增,在(-1,1)递减,在(1,$\frac{3}{2}$)递增,
故f(x)极大值=f(-1)=7-a,f(x)极小值=f(1)=3-a,
而f(-3)=-13-a,f($\frac{3}{2}$)=$\frac{31}{8}$-a,
故$\left\{\begin{array}{l}{f(-3)>0}\\{f(1)<0}\\{f(\frac{3}{2})≤0}\end{array}\right.$或$\left\{\begin{array}{l}{f(-3)<0}\\{f(0)>0}\\{f(1)=0}\end{array}\right.$,
解得:a∈$[{\frac{31}{8},7})∪\left\{3\right\}$,
故答案为:$[{\frac{31}{8},7})∪\left\{3\right\}$.
点评 本题考查了函数的单调性、极值、最值问题,考查导数的应用以及函数的零点问题,是一道中档题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:选择题
三棱锥S﹣ABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为( )
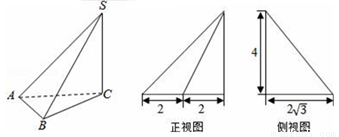
A.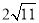 B.
B.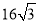 C.
C.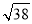 D.
D.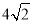
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $20+8\sqrt{2}$ | C. | 32 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7200种 | B. | 1440种 | C. | 1200种 | D. | 2880种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
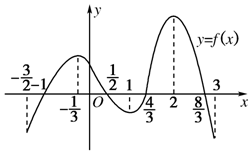 函数y=f(x)在定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
函数y=f(x)在定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )| A. | $[{-\frac{1}{3},1}]∪[2,3]$ | B. | $[{-1,\frac{1}{2}}]∪[{\frac{4}{3},\frac{8}{3}}]$ | ||
| C. | $[{-\frac{3}{2},\frac{1}{2}}]∪[1,2)$ | D. | $[{-\frac{3}{2},-\frac{1}{3}}]∪[{\frac{1}{2},\frac{4}{3}}]∪[{\frac{4}{3},3}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com