
| A. | 4 | B. | $20+8\sqrt{2}$ | C. | 32 | D. | 36 |
分析 利用向量的运算法则及两向量相等的公式可求出m,n;表示出(m-4)2+n2,据三角函数的有界性求出三角函数的最值.
解答 解:m$\overrightarrow{a}$+n$\overrightarrow{b}$=2$\overrightarrow{c}$,则m(1,-1)+n(1,1)=2($\sqrt{2}$cosα,$\sqrt{2}$sinα),
$\left\{\begin{array}{l}{m+n=2\sqrt{2}cosα}\\{-m+n=2\sqrt{2}sinα}\end{array}\right.$,则$\left\{\begin{array}{l}{m=\sqrt{2}(cosα-sinα)}\\{n=\sqrt{2}(cosα+sinα)}\end{array}\right.$,
由(m-4)2+n2=m2+n2-8m+16=2(cosα-sinα)2+2(cosα+sinα)-8$\sqrt{2}$(cosα-sinα)+16,
=2(1-2sinαcosα)+2(1+2sinαcosα)+16sin(α-$\frac{π}{4}$)+16,
=16sin(α-$\frac{π}{4}$)+20,
由-1≤sin(α-$\frac{π}{4}$)≤1,
4≤16sin(α-$\frac{π}{4}$)+20≤36,
∴4≤(m-4)2+n2≤36,
∴(m-4)2+n2的最大值36,
故选D.
点评 本题考查向量的运算法则,向量相等的坐标公式,以及三角函数的有界性,属于基础题.


科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:选择题
某一考点有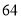 个试室,试室编号为
个试室,试室编号为 ,现根据试室号,采用系统抽样的方法,抽取
,现根据试室号,采用系统抽样的方法,抽取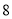 个试室进行监控抽查,已抽看了
个试室进行监控抽查,已抽看了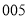 试室号,则下列可能被抽到的试室号是
试室号,则下列可能被抽到的试室号是
A.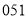 B.
B.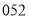 C.
C.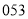 D.
D.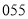
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | $[{\frac{{\sqrt{3}}}{2},1}]$ | C. | $[{\frac{1}{2},\frac{{\sqrt{3}}}{2}}]$ | D. | $[{\frac{1}{2},1}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
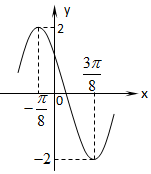 已知函数$f(x)=Asin(ωx+\frac{3π}{4})$(A>0,ω>0,|φ|<π)的一段图象如图所示,
已知函数$f(x)=Asin(ωx+\frac{3π}{4})$(A>0,ω>0,|φ|<π)的一段图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
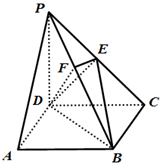 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,E是PC的中点,作EF⊥PB交PB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com