
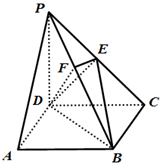
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,E是PC的中点,作EF⊥PB交PB于点F.分析 (1)连结AC,AC交BD于点G,连结EG,以D为原点,分别以$\overrightarrow{DA},\overrightarrow{DC},\overrightarrow{DP}$的方向为x轴,y轴,z轴的正方向,建立空间直角坐标系D-xyz,利用向量法能证明PA∥平面EDB.
(2)求出平面EFD的一个法向量和平面DEB的法向量,利用向量法能求出二面角F-DE-B的正弦值.
解答 证明:(1)连结AC,AC交BD于点G,连结EG.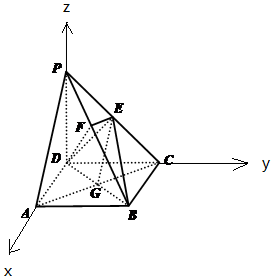
以D为原点,分别以$\overrightarrow{DA},\overrightarrow{DC},\overrightarrow{DP}$的方向为x轴,y轴,z轴的正方向,建立空间直角坐标系D-xyz,
依题意得$A(1,0,0),P(0,0,1),E(0,\frac{1}{2},\frac{1}{2})$.
因为底面ABCD是正方形,所以点G是此正方形的中心,
故点G的坐标为$(\frac{1}{2},\frac{1}{2},0)$,且$\overrightarrow{PA}=(1,0,-1),\overrightarrow{EG}=(\frac{1}{2},0,-\frac{1}{2})$.
所以$\overrightarrow{PA}=2\overrightarrow{EG}$,即PA∥EG,而EG?平面EDB,且PA?平面EDB,
因此PA∥平面EDB.----------------(6分)
解:(2)$B(1,1,0),\overrightarrow{PB}=(1,1,-1)$,又$\overrightarrow{DE}=(0,\frac{1}{2},\frac{1}{2})$,
故$\overrightarrow{PB}•\overrightarrow{DE}=0$,所以PB⊥DE.
由已知EF⊥PB,且EF∩DE=E,所以PB⊥平面EFD.----------------(7分)
所以平面EFD的一个法向量为$\overrightarrow{PB}=(1,1,-1)$.
$\overrightarrow{DE}=(0,\frac{1}{2},\frac{1}{2}),\overrightarrow{DB}=(1,1,0)$,
不妨设平面DEB的法向量为$\overrightarrow a=(x,y,z)$
则$\left\{\begin{array}{l}\overrightarrow a•\overrightarrow{DE}=\frac{1}{2}(y+z)=0\\ \overrightarrow a•\overrightarrow{DB}=x+y=0\end{array}\right.$
不妨取x=1则y=-1,z=1,即$\overrightarrow a=(1,-1,1)$----------------(10分)
设所求二面角F-DE-B的平面角为θ$cosθ=-\frac{{\overrightarrow a•\overrightarrow{PB}}}{{|\overrightarrow a||\overrightarrow{PB}|}}=\frac{1}{3}$,
因为θ∈[0,π],所以$sinθ=\frac{{2\sqrt{2}}}{3}$.
二面角F-DE-B的正弦值大小为$\frac{{2\sqrt{2}}}{3}$.----------------(12分)
点评 本题考查线面平行的证明,考查二面角的正弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、空间想象能力、运算求解能力,考查化归与转化思想、数形结合思想,是中档题.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向东南航行6km | B. | 向东南航行3$\sqrt{2}$km | C. | 向东北航行3$\sqrt{2}$km | D. | 向东北航行6km |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $20+8\sqrt{2}$ | C. | 32 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7200种 | B. | 1440种 | C. | 1200种 | D. | 2880种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:解答题
已知直线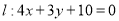 ,半径为
,半径为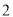 的圆
的圆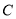 与
与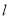 相切,圆心
相切,圆心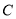 在
在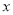 轴上且在直线
轴上且在直线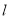 的右上方.
的右上方.
(1)求圆的方程;
(2)若直线过点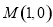 且与圆
且与圆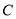 交于
交于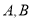 两点(
两点(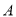 在
在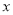 轴上方,B在
轴上方,B在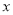 轴下方),问在
轴下方),问在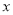 轴正半轴上是否存在定点
轴正半轴上是否存在定点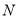 ,使得
,使得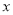 轴平分
轴平分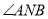 ?若存在,请求出点
?若存在,请求出点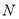 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com