
分析 (1)求出函数的导数,计算f′(0),求出a的值即可;
(2)求出函数的导数,通过讨论a的范围,求出函数的单调区间,求出函数的最小值,求出a的值即可;
(3)问题转化为-lnk<$ln({1+x})-\frac{x}{x+1}$,令a=1,则f(x)=$ln({1+x})-\frac{x}{x+1}$,根据函数的单调性求出k的范围即可.
解答 解:(1)∵$f'(x)=\frac{x+1-a}{{{{({x+1})}^2}}}$,∴f'(0)=1-a=5,∴a=-4.
(2)函数f(x)的定义域为(-1,+∞),$f'(x)=\frac{1}{1+x}-\frac{a}{{{{({x+1})}^2}}}$=$\frac{x+1-a}{{{{({x+1})}^2}}}$,
令f'(x)=0,则x=a-1,
①当a-1≤-1,即a≤0时,在(-1,+∞)上,f'(x)>0,函数f(x)单调递增,无最小值.
②当a-1>-1,即a>0时,在(-1,a-1)上,f'(x)<0,函数f(x)单调递减;
在(a-1,+∞)上,f'(x)>0,函数f(x)单调递增,
所以函数f(x)的最小值为f(a-1)=lna-a+1=-a,解得$a=\frac{1}{e}$.
综上,若函数f(x)的最小值为-a,则$a=\frac{1}{e}$.
(3)由(1+x)ln(1+x)+(lnk-1)x+lnk>0,
得,$ln({1+x})-\frac{x}{x+1}$+lnk>0,即-lnk<$ln({1+x})-\frac{x}{x+1}$,
令a=1,则f(x)=$ln({1+x})-\frac{x}{x+1}$,
由(1)可知,当a=1时,f(x)在(-1,0)上单调递减,在(0,+∞)上,f(x)单调递增,
所以在(-1,+∞)上,f(x)min=f(0)=0,所以-lnk<0,即k>1.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:选择题
在等差数列{an}中,已知a5=15,则a2+a4+a6+a8的值为( )
A.30 B.45 C.60 D.120
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
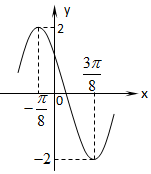 已知函数$f(x)=Asin(ωx+\frac{3π}{4})$(A>0,ω>0,|φ|<π)的一段图象如图所示,
已知函数$f(x)=Asin(ωx+\frac{3π}{4})$(A>0,ω>0,|φ|<π)的一段图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
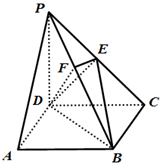 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,E是PC的中点,作EF⊥PB交PB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1≤x≤2} | B. | {x|x≥1} | C. | {x|1<x≤2} | D. | {x|2≤x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com