
分析 ①根据诱导公式化简即可;
②根据正切函数图象分析;
③求出整体$\frac{2}{3}$x+$\frac{π}{3}$的范围,结合函数的图象得出最值;
④根据对称轴过函数的最值点判断即可.
解答 解:①函数$y=cos(\frac{2}{3}x+\frac{7π}{2})$=sin$\frac{2}{3}$x是奇函数,正确;
②若α、β都是第一象限角且α<β,由正切函数图象可知tanα<tanβ错误,比如tan60°>tan390°,故错误;
③函数$y=2sin(\frac{2}{3}x+\frac{π}{3})$,x∈$[-π,\frac{π}{2}]$,则$\frac{2}{3}$x+$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],故最小值是-$\sqrt{3}$,最大值是2,故错误;
④直线$x=\frac{π}{8}$代入函数$y=\frac{1}{2}sin(5x+\frac{7π}{8})$=-$\frac{1}{2}$,成立,故是图象的一条对称轴.
故答案为①④.
点评 本题考查了三角函数图象的性质,属于基础题型,应熟练掌握.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:选择题
三棱锥P-A BC的四个顶点都在球D的表面上,PA⊥平面ABC,AB⊥BC,PA =3,AB=BC=2,则球O的表面积为( )
A.13π B.17π C.52π D.68π
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
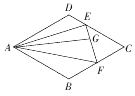 如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )
如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )| A. | $\frac{7}{9}$ | B. | $-\frac{2}{9}$ | C. | $-\frac{1}{9}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∠A和∠B都不是锐角 | B. | ∠A和∠B不都是锐角 | ||
| C. | ∠A和∠B都是钝角 | D. | ∠A和∠B都是直角 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 35 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com