
分析 (Ⅰ)由题意可得等比数列{an}的首项和公比都为2,等差数列{bn}的首项和公差都为2,运用等差数列和等比数列的通项公式,即可得到所求;
(Ⅱ)求得cn=an•bn=n•2n+1,运用数列的求和方法:错位相减法,结合等比数列的求和公式,化简整理即可得到所求和.
解答 解:(Ⅰ)等比数列{an}中,a1=2,an=2an-1(n≥2),
可得等比数列{an}的首项和公比都为2,
则an=2•2n-1=2n,n∈N*,
等差数列{bn}中,b1=2,点P(bn,bn+1)在一次函数y=x+2的图象上,
可得bn+1=bn+2,
等差数列{bn}的首项为2,公差为2,
可得bn=2+2(n-1)=2n,n∈N*;
(Ⅱ)cn=an•bn=n•2n+1,
则数列{cn}前n项和Tn=1•22+2•23+…+n•2n+1,
2Tn=1•23+2•24+…+(n-1)•2n+1+n•2n+2,
相减可得-Tn=22+23+…+2n+1-n•2n+2
=$\frac{4(1-{2}^{n})}{1-2}$-n•2n+2,
化简可得Tn=(n-1)•2n+2+4.
点评 本题考查等差数列和等比数列的定义和通项公式的运用,同时考查数列的求和方法:错位相减法,注意运用等比数列的求和公式,属于中档题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:解答题
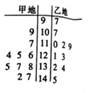 已知在一次期末数学测试中,教育局在某市甲、乙两地各抽取了10名学生的成绩做调查,所的情况如下所示.
已知在一次期末数学测试中,教育局在某市甲、乙两地各抽取了10名学生的成绩做调查,所的情况如下所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
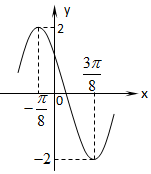 已知函数$f(x)=Asin(ωx+\frac{3π}{4})$(A>0,ω>0,|φ|<π)的一段图象如图所示,
已知函数$f(x)=Asin(ωx+\frac{3π}{4})$(A>0,ω>0,|φ|<π)的一段图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
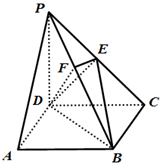 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,E是PC的中点,作EF⊥PB交PB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1≤x≤2} | B. | {x|x≥1} | C. | {x|1<x≤2} | D. | {x|2≤x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5份 | B. | 10份 | C. | 15份 | D. | 20份 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com