
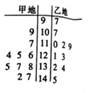
 已知在一次期末数学测试中,教育局在某市甲、乙两地各抽取了10名学生的成绩做调查,所的情况如下所示.
已知在一次期末数学测试中,教育局在某市甲、乙两地各抽取了10名学生的成绩做调查,所的情况如下所示.分析 (1)利用茎叶图能分别计算甲、乙两地这10名学生的平均成绩.
(2)以样本估计总体,利用茎叶图能估计甲、乙两地学生成绩的偏差程度.
(3)在甲地被抽取的10位同学中,成绩120分以上的有8人,其中2人的成绩在140人以上,由此利用等可能事件概率计算公式能求出恰有1名学生成绩在140分以上的概率.
解答 解:(1)甲地这10名学生的平均成绩$\overline{{x}_{甲}}$=$\frac{1}{10}$(109+117+124+125+126+135+137+138+142+147)=130,
乙地这10名学生的平均成绩$\overline{{x}_{乙}}$=$\frac{1}{10}$(97+107+110+112+119+121+123+132+134+145)=120.
(2)由茎叶图得到甲的成绩相对集中,乙的成绩相对分散,
∴甲地学生成绩的偏差程度小、乙地学生成绩的偏差程度大.
(3)在甲地被抽取的10位同学中,成绩120分以上的有8人,其中2人的成绩在140人以上,
∴从成绩120分以上的8位同学中随机抽取2人,基本事件总数n=${C}_{8}^{2}=28$,
恰有1名学生成绩在140分以上包含的基本事件个数m=${C}_{8}^{1}{C}_{2}^{1}=16$,
∴恰有1名学生成绩在140分以上的概率p=$\frac{m}{n}=\frac{16}{28}$=$\frac{4}{7}$.
点评 本题考查茎叶图、古典概型、概率等基础知识,考查数据处理能力、运算求解能力,考查函数与方程思想、集合思想,是基础题.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源:2016-2017学年江西省高一上学期第一次月考数学试卷(解析版) 题型:选择题
非空数集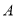 如果满足:①
如果满足:① ;②若对
;②若对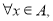 有
有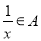 ,则称
,则称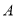 是“互倒集”.给出以下数集:
是“互倒集”.给出以下数集:
①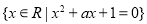 ;
;
②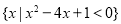 ;
;
③ .其中“互倒集”的个数是( )
.其中“互倒集”的个数是( )
A.0 B.3 C.2 D.1
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:填空题
已知高一年级有学生450人, 高二年级有学生750人, 高三年级有学生600人.用分层抽样从该校的这三个年级中抽取一个样本, 且每个学生被抽到的概率为0.02, 则应从高二年级抽取的学生人数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 121 | B. | 25 | C. | 31 | D. | 35 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{8}$ | B. | $\frac{5\sqrt{3}}{2}$ | C. | 10$\sqrt{3}$ | D. | $\frac{35}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向东南航行6km | B. | 向东南航行3$\sqrt{2}$km | C. | 向东北航行3$\sqrt{2}$km | D. | 向东北航行6km |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com