
| A. | 121 | B. | 25 | C. | 31 | D. | 35 |
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:解答题
设a1,d为实数,首项为a1,公差为d的等差数列{an}的前n项和为Sn,满足S5S6+15=0.
(1)若S5=5,求S6及a1;
(2)求d的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:选择题
在等差数列{an}中,已知a5=15,则a2+a4+a6+a8的值为( )
A.30 B.45 C.60 D.120
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
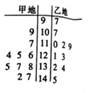 已知在一次期末数学测试中,教育局在某市甲、乙两地各抽取了10名学生的成绩做调查,所的情况如下所示.
已知在一次期末数学测试中,教育局在某市甲、乙两地各抽取了10名学生的成绩做调查,所的情况如下所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间(t) | 2 | 4 | 6 | 8 | 10 |
| 日销售量(y) | 38 | 37 | 32 | 33 | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com