
| A. | $\frac{5}{8}$ | B. | $\frac{5\sqrt{3}}{2}$ | C. | 10$\sqrt{3}$ | D. | $\frac{35}{8}$ |
分析 由已知可得a=$\frac{5}{2}$,b=$\frac{7}{2}$,c=$\frac{8}{2}=4$,代入S=$\sqrt{\frac{1}{4}[{c}^{2}{a}^{2}-(\frac{{c}^{2}+{a}^{2}-{b}^{2}}{2})^{2}]}$,即可.
解答 解:周长为10的△ABC满足sinA:sinB:sinC=5:7:8,
则其三边a,b,c满足a:b:c=5:7:8,
设a=5k,b=7k,c=8k,则5k+7k+8k=10,∴a=$\frac{5}{2}$,b=$\frac{7}{2}$,c=$\frac{8}{2}=4$,
代入S=$\sqrt{\frac{1}{4}[{c}^{2}{a}^{2}-(\frac{{c}^{2}+{a}^{2}-{b}^{2}}{2})^{2}]}$,
得s=$\frac{5\sqrt{3}}{2}$,
故选:B
点评 本题考查了正弦定理,解题的关键是要读懂题意,转化条件,属于基础题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:选择题
某一考点有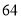 个试室,试室编号为
个试室,试室编号为 ,现根据试室号,采用系统抽样的方法,抽取
,现根据试室号,采用系统抽样的方法,抽取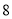 个试室进行监控抽查,已抽看了
个试室进行监控抽查,已抽看了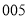 试室号,则下列可能被抽到的试室号是
试室号,则下列可能被抽到的试室号是
A.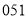 B.
B.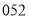 C.
C.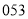 D.
D.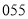
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
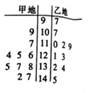 已知在一次期末数学测试中,教育局在某市甲、乙两地各抽取了10名学生的成绩做调查,所的情况如下所示.
已知在一次期末数学测试中,教育局在某市甲、乙两地各抽取了10名学生的成绩做调查,所的情况如下所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
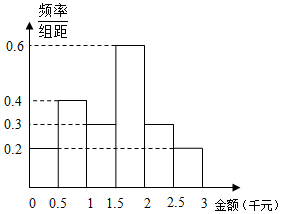 某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:
某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:| 网购达人 | 非网购达人 | 合计 | |
| 男性 | 30 | ||
| 女性 | 12 | 30 | |
| 合计 | 60 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | $[{\frac{{\sqrt{3}}}{2},1}]$ | C. | $[{\frac{1}{2},\frac{{\sqrt{3}}}{2}}]$ | D. | $[{\frac{1}{2},1}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com