已知向量$\overrightarrow a=(4.2).\overrightarrow b=(x.3)$.且$\overrightarrow a⊥\overrightarrow b$.则x的值是-$\frac{3}{2}$．题目和参考答案——青夏教育精英家教网—

14．已知向量$\overrightarrow a=（4，2），\overrightarrow b=（x，3）$，且$\overrightarrow a⊥\overrightarrow b$，则x的值是-$\frac{3}{2}$．

分析根据题意，由于$\overrightarrow a⊥\overrightarrow b$，则有$\overrightarrow{a}$•$\overrightarrow{b}$=0，将$\overrightarrow{a}$、$\overrightarrow{b}$的坐标代入计算即可得答案．

解答解：根据题意，向量$\overrightarrow a=（4，2），\overrightarrow b=（x，3）$，
若$\overrightarrow a⊥\overrightarrow b$，则有$\overrightarrow{a}$•$\overrightarrow{b}$=4x+6=0，
解可得x=-$\frac{3}{2}$；
故答案为：-$\frac{3}{2}$．

点评本题考查向量的数量积的坐标计算，注意向量垂直即两向量的数量积为0．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源：2016-2017学年河南省新乡市高二上学期入学考数学卷（解析版） 题型：填空题

对于函数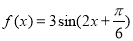，给出下列命题：

①图像关于原点成中心对称

②图像关于直线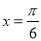对称

③函数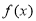的最大值是3

④函数的一个单调增区间是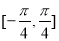

其中正确命题的序号为．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

5．已知椭圆C：$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1，A，B分别为椭圆C的左、右顶点，F₁，F₂为其左、右焦点．
（Ⅰ）若点Q为椭圆C的上顶点，求△QF₁F₂内切圆的面积；
（Ⅱ）若斜率为k，过定点F₂的直线l与椭圆C交于M，N两点，试证明：直线AM、直线BN与直线x=4三线必定共点．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

2．《数书九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白，与著名的海伦公式完全等价，由此可以看出我国古代具有很高的数学水平，其求法是“以小斜幂，并大斜幂，减中斜幂，余半之，自乘于上．以小斜幂乘大斜幂，减上，余四约之，为实，一为从偶，开平方得积”，若把这段文字写成公式，即S=$\sqrt{\frac{1}{4}[{c}^{2}{a}^{2}-（\frac{{c}^{2}+{a}^{2}-{b}^{2}}{2}）^{2}]}$，现有周长为10的△ABC满足sinA：sinB：sin：C=5：7：8，试用以上给出的公式求得△ABC的面积为（　　）

A．

$\frac{5}{8}$

B．

$\frac{5\sqrt{3}}{2}$

C．

10$\sqrt{3}$

D．

$\frac{35}{8}$

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

9．y=$tan（4x+\frac{π}{3}）$的最小正周期是（　　）

A．

$\frac{π}{4}$

B．

$\frac{π}{2}$

C．

D．

2π

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

19．（Ⅰ）化简：$\frac{{{{sin}^2}（α-\frac{π}{2}）}}{{cos（α-3π）+sin（\frac{3π}{2}+α）}}$
（Ⅱ）计算：sin30°cos60°+tan45°cos90°-sin180°cos270°．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

5．已知向量$\overrightarrow a$表示“向东航行3km”，向量$\overrightarrow b$表示“向南航行3km，则$\overrightarrow a$+$\overrightarrow b$表示（　　）

A．

向东南航行6km

B．

向东南航行3$\sqrt{2}$km

C．

向东北航行3$\sqrt{2}$km

D．

向东北航行6km

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

2．（文）已知向量$\overrightarrow{a}$=（1，-1），$\overrightarrow{b}$=（1，1），$\overrightarrow{c}$=（$\sqrt{2}$cosα，$\sqrt{2}$sinα）（a∈R），实数m，n满足m$\overrightarrow{a}$+n$\overrightarrow{b}$=2$\overrightarrow{c}$，则（m-4）²+n²的最大值为（　　）

A．

B．

$20+8\sqrt{2}$

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

2．已知函数f（x）=e^x，g（x）=mx²+ax+b，其中m，a，b∈R，e=2.71828…为自然对数的底数．
（I）函数h（x）=xf （x），当a=l，b=0时，若函数h（x）与g（x）具有相同的单调区间，求m的值；
（II）记F（x）=f（x）-g（x）．当a=2，m=0时，若函数F（x）在[-1，2]上存在两个不同的零点，求b的取值范围．

查看答案和解析>>

同步练习册答案