
分析 (I)△QF1F2为等边三角形,故其内切圆半径为$\frac{1}{3}$OQ=$\frac{1}{3}$b,再代入面积公式计算;
(II)联立方程组,得出AM,BN的方程,求出它们与直线x=4的交点坐标,借助根与系数的关系证明交点重合即可.
解答 解:(I)Q(0,$\sqrt{3}$),F1(-1,0),F2(1,0),
∴QF1=QF2=F1F2=2,即△QF1F2是边长为2的等边三角形,
∴△QF1F2内切圆半径r=$\frac{1}{3}$OQ=$\frac{\sqrt{3}}{3}$,
∴△QF1F2内切圆面积为S=π•$\frac{1}{3}$=$\frac{π}{3}$.
(II)直线l的方程为y=k(x-1),代入椭圆方程得:(3+4k2)x2-8k2x+4(k2-3)=0,
设M(x1,y1),N(x2,y2),则x1+x2=$\frac{8{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{4({k}^{2}-3)}{3+4{k}^{2}}$,
又A(-2,0),B(2,0),
∴直线AM的方程为:y=$\frac{{y}_{1}}{{x}_{1}+2}$(x+2),令x=4得y=$\frac{6{y}_{1}}{{x}_{1}+2}$=$\frac{6k({x}_{1}-1)}{{x}_{1}+2}$,
即直线AM与直线x=4的交点坐标为D(4,$\frac{6k({x}_{1}-1)}{{x}_{1}+2}$)
直线BN的方程为y=$\frac{{y}_{2}}{{x}_{2}-2}$(x-2),令x=4得y=$\frac{2{y}_{2}}{{x}_{2}-2}$=$\frac{2k({x}_{2}-1)}{{x}_{2}-2}$,
即直线BN与直线x=4的交点坐标为E(4,$\frac{2k({x}_{2}-1)}{{x}_{2}-2}$),
$\frac{6k({x}_{1}-1)}{{x}_{1}+2}$-$\frac{2k({x}_{2}-1)}{{x}_{2}-2}$=$\frac{6k({x}_{1}-1)({x}_{2}-2)-2k({x}_{2}-1)({x}_{1}+2)}{({x}_{1}+2)({x}_{2}-2)}$=$\frac{4k{x}_{1}{x}_{2}-10k({x}_{1}+{x}_{2})+16k}{({x}_{1}+2)({x}_{2}-2)}$,
∵4kx1x2-10k(x1+x2)+16k=$\frac{16k({k}^{2}-3)}{3+4{k}^{2}}$-$\frac{80{k}^{3}}{3+4{k}^{2}}$+16k=0,
∴点D与点E重合,
∴直线AM、直线BN与直线x=4三线必定共点.
点评 本题考查了椭圆的性质,直线与椭圆的位置关系,注意根与系数关系的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
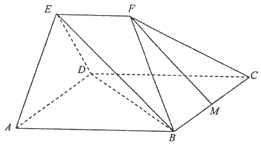 已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.
已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:选择题
某一考点有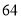 个试室,试室编号为
个试室,试室编号为 ,现根据试室号,采用系统抽样的方法,抽取
,现根据试室号,采用系统抽样的方法,抽取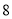 个试室进行监控抽查,已抽看了
个试室进行监控抽查,已抽看了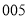 试室号,则下列可能被抽到的试室号是
试室号,则下列可能被抽到的试室号是
A.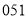 B.
B.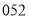 C.
C.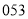 D.
D.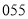
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:选择题
在等差数列{an}中,已知a5=15,则a2+a4+a6+a8的值为( )
A.30 B.45 C.60 D.120
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
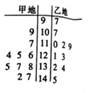 已知在一次期末数学测试中,教育局在某市甲、乙两地各抽取了10名学生的成绩做调查,所的情况如下所示.
已知在一次期末数学测试中,教育局在某市甲、乙两地各抽取了10名学生的成绩做调查,所的情况如下所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
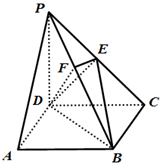 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,E是PC的中点,作EF⊥PB交PB于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com