
| A. | (-6,2) | B. | (6,-2) | C. | (-2,0) | D. | (2,0) |
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 二分法是求方程近似解的一种方法,其原理是“一分为二、无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.05,则输出n的值为( )
二分法是求方程近似解的一种方法,其原理是“一分为二、无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.05,则输出n的值为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
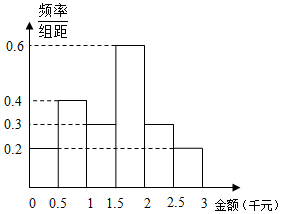 某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:
某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:| 网购达人 | 非网购达人 | 合计 | |
| 男性 | 30 | ||
| 女性 | 12 | 30 | |
| 合计 | 60 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | $-\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com