
分析 根据正弦型函数$f(x)=4sin(2x+\frac{π}{3}),x∈$R的图象与性质,
对题目中的命题判断正误即可.
解答 解:对于函数$f(x)=4sin(2x+\frac{π}{3}),x∈$R,
函数y=f(x)的初相是$\frac{π}{3}$,①错误;
x=$\frac{π}{6}$,f(x)=4sin(2×$\frac{π}{6}$+$\frac{π}{3}$)=2$\sqrt{3}$≠0,
∴函数y=f(x)的图象不关于点$({\frac{π}{6},0})$对称,②错误;
x=$\frac{π}{12}$,f(x)=4sin(2×$\frac{π}{12}$+$\frac{π}{3}$)=4,
∴函数y=f(x)的图象关于直线$x=\frac{π}{12}$对称,③正确.
综上,正确的命题是③.
故答案为:③.
点评 本题考查了正弦型函数的图象与性质的应用问题,是基础题.


科目:高中数学 来源:2016-2017学年河南省新乡市高二上学期入学考数学卷(解析版) 题型:填空题
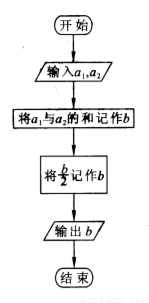
图中所示的是一个算法的流程图,已知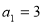 ,输出的
,输出的 ,则
,则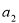 的值是___________.
的值是___________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 超市 | A | B | C | D | E | F | G |
| 广告费支出xi | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
| 销售额yi | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-6,2) | B. | (6,-2) | C. | (-2,0) | D. | (2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-6,2) | B. | (6,-2) | C. | (-2,0) | D. | (2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,+∞) | B. | $({\frac{1}{2},+∞})$ | C. | $({-∞,-\frac{1}{2}})$ | D. | $({-\frac{1}{2},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com