
分析 (1)圆:x2+y2+Dx+Ey+F=0的圆心(-$\frac{D}{2}$,-$\frac{E}{2}$),半径=$\frac{1}{2}\sqrt{{D}^{2}+{E}^{2}-4F}$,由此能求出两圆的圆心和半径,再求出圆心距,利用圆心距和两圆半径的关系能判断圆C1与圆C2的位置关系.
(2)点A(-1,1)在圆C2:x2+y2-4x-4y-2=0上,求出${k}_{A{C}_{2}}$=$\frac{1}{3}$,从而直线l的斜率k=-$\frac{1}{{k}_{A{C}_{2}}}$=-3,由此能求出直线l的方程.
解答 解:(1)圆C1:x2+y2+2x+8y-8=0的圆心C1(-1,-4),半径r1=$\frac{1}{2}\sqrt{4+64+32}$=5,
圆C2:x2+y2-4x-4y-2=0的圆心C2(2,2),半径r2=$\frac{1}{2}\sqrt{16+16+8}$=$\sqrt{10}$,
|C1C2|=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$,
∴|r1-r2|<|C1C2|<r1+r2,
∴圆C1与圆C2相交.
(2)点A(-1,1)在圆C2:x2+y2-4x-4y-2=0上,
${k}_{A{C}_{2}}$=$\frac{2-1}{2+1}$=$\frac{1}{3}$,
∵经过点A(-1,1)的直线1与圆C2相切,
∴直线l的斜率k=-$\frac{1}{{k}_{A{C}_{2}}}$=-3,
∴直线l的方程为y-1=-3(x+1),即3x+y+2=0.
点评 本题考查圆、直线方程、两点间距离公式、斜率公式、切线等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是中档题.


科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:选择题
某程序的框图如图所示,执行该程序,若输入的N=5,则输出i=( )
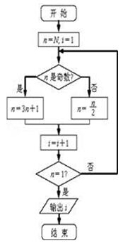
A.9 B.8 C.7 D.6
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{3}{2}$,$\frac{5}{3}$] | B. | [$\frac{5}{6}$,$\frac{3}{2}$] | C. | [$\frac{5}{6}$,+∞) | D. | [$\frac{5}{6}$,$\frac{5}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 二分法是求方程近似解的一种方法,其原理是“一分为二、无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.05,则输出n的值为( )
二分法是求方程近似解的一种方法,其原理是“一分为二、无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.05,则输出n的值为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1) | B. | (2) | C. | (3) | D. | (4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com