
| A. | [$\frac{3}{2}$,$\frac{5}{3}$] | B. | [$\frac{5}{6}$,$\frac{3}{2}$] | C. | [$\frac{5}{6}$,+∞) | D. | [$\frac{5}{6}$,$\frac{5}{3}$] |
分析 根据余弦函数的图象与性质,结合题意得出π≤ωπ+$\frac{π}{6}$≤$\frac{11π}{6}$,
从而求出ω的取值范围.
解答 解:函数f(x)=cos(ωx+$\frac{π}{6}$)(ω>0),
当x∈[0,π]时,f(x)∈[-1,$\frac{\sqrt{3}}{2}$],
∴-1≤cos(ωx+$\frac{π}{6}$)≤$\frac{\sqrt{3}}{2}$,画出图形如图所示;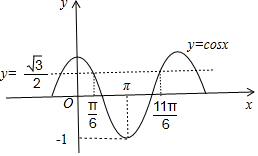
则π≤ωπ+$\frac{π}{6}$≤$\frac{11π}{6}$,
解得$\frac{5}{6}$≤ω≤$\frac{5}{3}$,
∴ω的取值范围是[$\frac{5}{6}$,$\frac{5}{3}$].
故选:D.
点评 本题考查了余弦函数的图象与性质的应用问题,是基础题.


科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:解答题
执行如下程序框图:
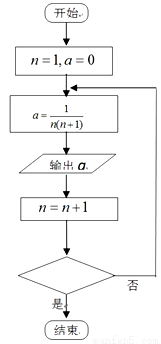
(1)如果在判断框内填入“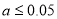 ”,请写出输出的所有数值;
”,请写出输出的所有数值;
(2)如果在判断框内填入“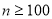 ”,试求出所有输出数字的和。
”,试求出所有输出数字的和。
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 超市 | A | B | C | D | E | F | G |
| 广告费支出xi | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
| 销售额yi | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com