
| ���� | A | B | C | D | E | F | G |
| ����֧��xi | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
| ���۶�yi | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
���� ���������⣬����ع�ϵ����д�����Իع鷽�̣�
������R2�ľ���ֵԽ�ӽ�1��ģ��Ч��Խ�ã��ó����κ����ع�ģ�����ʣ�
���ö��κ���ģ�����x=3ʱy��ֵ���ɣ�
��� �⣺����$\overline x=8��\overline y=42��\sum_{i=1}^7{x_i}{y_i}=2794��\sum_{i=1}^7{{x_i}^2}$=708��
��ع�ϵ��Ϊ$\hat b=\frac{{\sum_{i=1}^n{x_i}{y_i}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$=$\frac{2794-7��8��42}{{708-7��{8^2}}}=1.7$������3�֣�
$\hat a=\overline y-\hat b\overline x=28.4$������5�֣�
��y����x�����Իع鷽����$\overline y=1.7x+28.4$������6�֣�
����R2�ֱ�ԼΪ0.93��0.75����0.75��0.93��
����κ����ع�ģ�����ʣ�����9�֣�
��x=3��Ԫʱ��$\hat y=-0.17{x^2}$+5x+20=-0.17��32+5��3+20=33.47��
��Ԥ��A�������۶�Ϊ33.47��Ԫ������12�֣�
���� ���⿼���˻ع鷽�̵�����Ӧ�����⣬��ȷ�����ǽ���Ĺؼ������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꽭��ʡ��һ��ѧ�ڵ�һ���¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
��֪����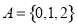 ��
��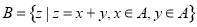 ����
����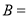 �� ��
�� ��
A��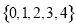 B��
B��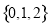 C��
C��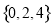 D��
D��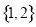
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ��ӱ�ʡ�߶����ϵ�һ���¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
ij����Ŀ�ͼ��ͼ��ʾ��ִ�иó����������N=5�������i=�� ��
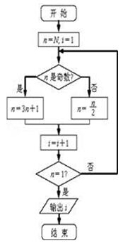
A��9 B��8 C��7 D��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [$\frac{3}{2}$��$\frac{5}{3}$] | B�� | [$\frac{5}{6}$��$\frac{3}{2}$] | C�� | [$\frac{5}{6}$��+�ޣ� | D�� | [$\frac{5}{6}$��$\frac{5}{3}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ���ַ����̽��ƽ��һ�ַ�������ԭ���ǡ�һ��Ϊ�������ޱƽ�����ִ����ͼ��ʾ�ij����ͼ��������x1=1��x2=2��d=0.05�������n��ֵΪ��������
���ַ����̽��ƽ��һ�ַ�������ԭ���ǡ�һ��Ϊ�������ޱƽ�����ִ����ͼ��ʾ�ij����ͼ��������x1=1��x2=2��d=0.05�������n��ֵΪ��������| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-6��1�� | B�� | ��6��-1�� | C�� | ��6��1�� | D�� | ��-6��-1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �ڢ� | C�� | �٢� | D�� | �ڢ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com