
分析 在单位圆内画出对应的正弦函数线,根据正弦线求出-$\frac{2π}{3}$≤θ≤$\frac{π}{6}$时sinθ的取值范围.
解答 解:-$\frac{2π}{3}$≤θ≤$\frac{π}{6}$,在单位圆内画出对应的正弦函数线,如图所示;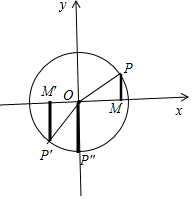
则-$\frac{2π}{3}$对应的正弦线为$\overrightarrow{M′P′}$,正弦值为-$\frac{\sqrt{3}}{2}$;
$\frac{π}{6}$对应的正弦线为$\overrightarrow{PM}$,正弦值为$\frac{1}{2}$,
其中-$\frac{π}{2}$对应的正弦值线为$\overrightarrow{OP″}$,正弦值为-1,
利用三角函数线,可得-$\frac{2π}{3}$≤θ≤$\frac{π}{6}$时,
sinθ的取值范围是[-1,$\frac{1}{2}$].
故答案为:[-1,$\frac{1}{2}$].
点评 本题考查了单位圆与正弦函数线的应用问题,是基础题.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河南省新乡市高二上学期入学考数学卷(解析版) 题型:选择题
为了得到函数 的图像,只需将
的图像,只需将 的图像上每一点
的图像上每一点
A.向左平移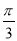 个单位长度
个单位长度
B.向右平移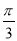 个单位长度
个单位长度
C.向左平移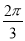 个单位长度
个单位长度
D.向右平移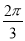 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:选择题
三棱锥S﹣ABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为( )
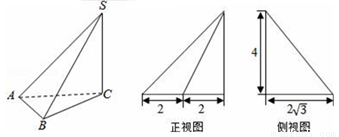
A.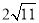 B.
B.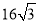 C.
C.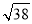 D.
D.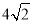
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 3 | C. | $\sqrt{5}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-6,2) | B. | (6,-2) | C. | (-2,0) | D. | (2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com