
【题目】已知正三角形![]() 的边长为2,
的边长为2,![]() 是边
是边![]() 的中点,动点
的中点,动点![]() 满足
满足![]() ,且
,且![]() ,其中
,其中![]() ,则
,则![]() 的最大值为( )
的最大值为( )
A.1B.![]() C.2D.
C.2D.![]()
【答案】D
【解析】
可建立如图所示的平面直角坐标系,根据题设条件可得动点![]() 在图中的圆上(实线部分)运动,设点
在图中的圆上(实线部分)运动,设点![]() ,则可用
,则可用![]() 的三角函数表示
的三角函数表示![]() ,从而可求其最大值.也可以把
,从而可求其最大值.也可以把![]() 表示为
表示为![]() ,故
,故![]() (如图),利用向量共线的几何意义可得
(如图),利用向量共线的几何意义可得![]() 的最大值就是
的最大值就是![]() 的最大值,利用三角形相似得当
的最大值,利用三角形相似得当![]() 与半圆相切时
与半圆相切时![]() 最大.
最大.
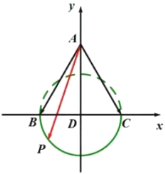
如图所示,由于动点![]() 满足
满足![]() ,且
,且![]() ,
,
因为![]() ,所以点
,所以点![]() 在以点
在以点![]() 为圆心,1为半径的半圆(图中实线)上运动,
为圆心,1为半径的半圆(图中实线)上运动,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以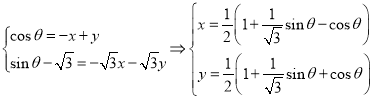 ,
,
![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() .
.
所以![]() ,故选D.
,故选D.
方法二:等和线法
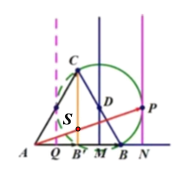
由于动点![]() 满足
满足![]() ,且
,且![]() ,其中
,其中![]() ,
,
所以点![]() 在以点
在以点![]() 为圆心,1为半径的半圆(图中实线)上运动且
为圆心,1为半径的半圆(图中实线)上运动且![]() .
.
设![]() 的中点为
的中点为![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,
![]() ,
,
所以![]() ,所以
,所以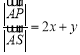 ,
,
过点![]() 分别作直线平行
分别作直线平行![]() 交
交![]() 于
于![]() ,
,
则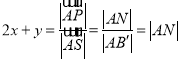 ,当
,当![]() 与半圆相切时,
与半圆相切时,![]() 最大且为
最大且为![]() .
.
故选D.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】现有7道题,其中5道甲类题,2道乙类题,张同学从中任取2道题解答.试求:
(1)所取的两道题都是甲类题的概率;
(2)所取的两道题不是同一类题的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市旅游局为了进一步开发旅游资源,需要了解游客的情况,以便制定相应的策略,在某月中随机抽取甲、乙两个景点各10天的游客数,画出茎叶图如下:若景点甲中的数据的中位数是126,景点乙中的数据的平均数是124.
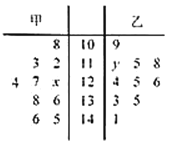
(1)求![]() ,
,![]() 的值;
的值;
(2)若将图中景点甲中的数据作为该景点较长一段时期内的样本数据(视样本频率为概率).今从这段时期内任取4天,记其中游客数不低于125人的天数为![]() ,求概率
,求概率![]() ;
;
(3)现从上图的共20天的数据中任取2天的数据(甲、乙两景点中各取1天),记其中游客数不低于115且不高于135人的天数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问題:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马、“马主曰:“我马食半牛,”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟、羊主人说:“我羊所吃的禾苗只有马的一半,”马主人说:“我马所吃的禾苗只有牛的一半,“打算按此比例偿还,他们各应偿还多少?该问题中,1斗为10升,则马主人应偿还( )升粟?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列三个命题:
①若![]() ,则
,则![]() 或
或![]() 的逆命题;
的逆命题;
②若![]() ,则
,则![]() 的逆否命题;
的逆否命题;
③若![]() 、
、![]() ,
,![]() 是奇数,则
是奇数,则![]() 、
、![]() 中一个是奇数,一个是偶数.
中一个是奇数,一个是偶数.
其中真命题的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com