
【题目】已知以点![]()
![]() (
(![]() ,且
,且![]() )为圆心的圆与
)为圆心的圆与![]() 轴交于点
轴交于点![]() ,
, ![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
, ![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)求证: ![]() 的面积为定值;
的面积为定值;
(2)设直线![]() 与圆
与圆![]() 交于点
交于点![]() ,
, ![]() ,若
,若![]() ,求圆
,求圆![]() 的方程.
的方程.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】以下几个结论中:①在△ABC中,有等式 ![]() ②在边长为1的正△ABC中一定有
②在边长为1的正△ABC中一定有 ![]() =
= ![]()
③若向量 ![]() =(﹣3,2),
=(﹣3,2), ![]() =(0,﹣1),则向量
=(0,﹣1),则向量 ![]() 在向量
在向量 ![]() 方向上的投影是﹣2
方向上的投影是﹣2
④与向量 ![]() =(﹣3,4)同方向的单位向量是
=(﹣3,4)同方向的单位向量是 ![]() =(﹣
=(﹣ ![]() ,
, ![]() )
)
⑤若a=40,b=20,B=25°,则满足条件的△ABC仅有一个;
其中正确结论的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某种算法的程序,回答下面的问题:
(1)写出输出值y关于输入值x的函数关系式f (x);
(2)当输出的y值小于![]() 时,求输入的x的取值范围.
时,求输入的x的取值范围.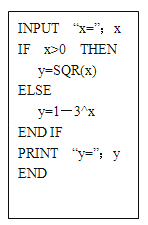
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若直线![]() 与曲线
与曲线![]() 都只有两个交点,证明:这四个交点可以构成一个平行四边形,并计算该平行四边形的面积;
都只有两个交点,证明:这四个交点可以构成一个平行四边形,并计算该平行四边形的面积;
(2)设函数![]() 在[1,2]上的值域为
在[1,2]上的值域为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() :
: ![]() (
(![]() )上,设
)上,设![]() ,
, ![]() ,
, ![]() 分别为左顶点、上顶点、下顶点,且下顶点
分别为左顶点、上顶点、下顶点,且下顶点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设点![]() ,
, ![]() (
(![]() )为椭圆
)为椭圆![]() 上两点,且满足
上两点,且满足![]() ,求证:
,求证: ![]() 的面积为定值,并求出该定值.
的面积为定值,并求出该定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com