
【题目】如图,四棱锥![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() .
.
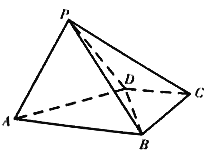
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格,某校有800名学生参加了初赛,所有学生的成绩均在区间(30,150]内,其频率分布直方图如图.则获得复赛资格的人数为()

A.640B.520C.280D.240
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组调查学生使用智能手机对学习成绩的影响,部分统计数据如下表:
使用智能手机 | 不使用智能手机 | 总计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
总计 | 20 | 10 | 30 |
(Ⅰ)根据以上![]() 列联表判断,能否在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响?
列联表判断,能否在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响?
(Ⅱ)从学习成绩优秀的12名同学中,随机抽取2名同学,求抽到不使用智能手机的人数![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.05 | 0,。025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax+bx﹣cx , 其中c>a>0,c>b>0.
(1)记集合M={(a,b,c)|a,b,c不能构成一个三角形的三条边长,且a=b},则(a,b,c)∈M所对应的f(x)的零点的取值集合为 .
(2)若a,b,c是△ABC的三条边长,则下列结论正确的是 . (写出所有正确结论的序号)
①x∈(﹣∞,1),f(x)>0;
②x∈R,使ax , bx , cx不能构成一个三角形的三条边长;
③若△ABC为钝角三角形,则x∈(1,2),使f(x)=0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(x﹣ ![]() )+cos(x﹣
)+cos(x﹣ ![]() ),g(x)=2sin2
),g(x)=2sin2 ![]() .
.
(1)若α是第一象限角,且f(α)= ![]() ,求g(α)的值;
,求g(α)的值;
(2)求使f(x)≥g(x)成立的x的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直棱柱ABCD﹣A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3. 
(1)证明:AC⊥B1D;
(2)求直线B1C1与平面ACD1所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示: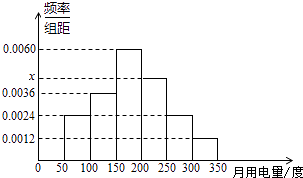
(Ⅰ)直方图中x的值为;
(Ⅱ)在这些用户中,用电量落在区间[100,250)内的户数为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com