练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某市举行“中学生诗词大赛”，分初赛和复赛两个阶段进行，规定：初赛成绩大于90分的具有复赛资格，某校有800名学生参加了初赛，所有学生的成绩均在区间（30，150]内，其频率分布直方图如图．则获得复赛资格的人数为（）

    A.640B.520C.280D.240

    【答案】B

    【解析】

    由频率分布直方图得到初赛成绩大于90分的频率，由此能求出获得复赛资格的人数．

    初赛成绩大于90分的具有复赛资格，某校有800名学生参加了初赛，

    所有学生的成绩均在区间（30，150]内，

    由频率分布直方图得到初赛成绩大于90分的频率为：1﹣（0.0025+0.0075+0.0075）×20＝0.65．

    ∴获得复赛资格的人数为：0.65×800＝520．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】若对任意实数都有函数的图象与直线相切，则称函数为“恒切函数”，设函数，其中.

    （1）讨论函数的单调性；

    （2）已知函数为“恒切函数”，

    ①求实数的取值范围；

    ②当取最大值时，若函数也为“恒切函数”，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝4x2－kx－8.

    (1)若函数y＝f(x)在区间[2,10]上单调，求实数k的取值范围；

    (2)若y＝f(x)在区间(－∞，2]上有最小值－12，求实数k的值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若将函数f（x）=sin（2x+ ）的图象向右平移个单位长度，可以使f（x）成为奇函数，则的最小值为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着旅游观念的转变和旅游业的发展，国民在旅游休闲方面的投入不断增多，民众对旅游的需求也不断提高，安庆某社区居委会统计了2011至2015年每年春节期间外出旅游的家庭数，具体统计资料如表：

    年份（x）

    2011

    2012

    2013

    2014

    2015

    家庭数（y）

    6

    10

    16

    22

    26


    （1）从这5年中随机抽取两年，求外出旅游的家庭至少有1年多于20个的概率；
    （2）利用所给数据，求出春节期间外出旅游的家庭数与年份之间的回归直线方程 ，并判断它们之间是正相关还是负相关；
    （3）利用（2）中所求出的回归直线方程估计该社区2016年在春节期间外出旅游的家庭数．
    参考公式： ， ．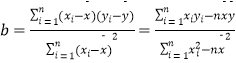

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】正方形和内接于同一个直角三角形ABC中，如图所示，设，若两正方形面积分别为=441，=440，则=______

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，直线l的方程为x﹣y+4=0，曲线C的参数方程 （α为参数）
    （1）已知在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，点P的极坐标 ，判断点P与直线l的位置关系；
    （2）设点Q为曲线C上的一个动点，求它到直线l的距离的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设{an}是首项为a，公差为d的等差数列（d≠0），Sn是其前n项和．记bn= ，n∈N* ， 其中c为实数．
    （1）若c=0，且b1 ， b2 ， b4成等比数列，证明：Snk=n2Sk（k，n∈N*）；
    （2）若{bn}是等差数列，证明：c=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥，底面为直角梯形，，，，.

    （1）求证：平面平面；

    （2）若直线与平面所成角为，求直线与平面所成角的正弦值.

    查看答案和解析>>

    同步练习册答案