
分析 根据题意,在同一坐标系中画出函数f(x)=sinx和$g(x)=cos(x-\frac{π}{3})$的图象,
其中x∈[-π,π],根据函数图象即可得出结论.
解答 解:在同一坐标系中画出函数f(x)=sinx和$g(x)=cos(x-\frac{π}{3})$的图象,
其中x∈[-π,π],如图所示;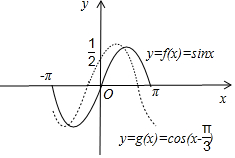
则f(x)的图象上存在2个点关于y轴对称,分别是(-π,0)和(π,0)与(0,0);
g(x)的图象上存在2个点关于y轴对称,分别是(-π,-$\frac{\sqrt{3}}{2}$)和(π,-$\frac{\sqrt{3}}{2}$)与($\frac{1}{2}$,0).
故答案为:2.
点评 本题考查了正弦函数与余弦函数的图象与性质的应用问题,是基础题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:选择题
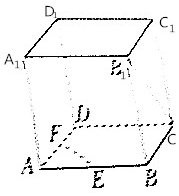 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
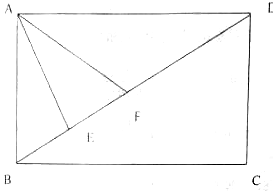 小王大学毕业后决定利用所学知识自主创业,在一块矩形的空地上办起了养殖场,如图所示,四边形ABCD为矩形,AB=200米,AD=200$\sqrt{3}$米,现为了养殖需要,在养殖场内要建造蓄水池,小王因地制宜,建造了一个三角形形状的蓄水池,其中顶点分别为A,E,F(E,F两点在线段BD上),且∠EAF=$\frac{π}{6}$,设∠BAE=α.
小王大学毕业后决定利用所学知识自主创业,在一块矩形的空地上办起了养殖场,如图所示,四边形ABCD为矩形,AB=200米,AD=200$\sqrt{3}$米,现为了养殖需要,在养殖场内要建造蓄水池,小王因地制宜,建造了一个三角形形状的蓄水池,其中顶点分别为A,E,F(E,F两点在线段BD上),且∠EAF=$\frac{π}{6}$,设∠BAE=α.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
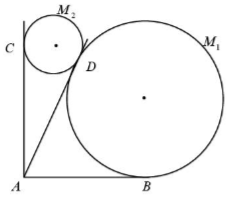 某景区欲建两条圆形观景步道M1,M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M与AB,AD分别相切于点B,D,圆M2与AC,AD分别相切于点C,D.
某景区欲建两条圆形观景步道M1,M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M与AB,AD分别相切于点B,D,圆M2与AC,AD分别相切于点C,D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(\frac{1}{2})<f(-\frac{3}{2})<f(3)$ | B. | $f(3)<f(-\frac{3}{2})<f(\frac{1}{2})$ | C. | $f(\frac{1}{2})<f(3)<f(-\frac{3}{2})$ | D. | $f(3)<f(\frac{1}{2})<f(-\frac{3}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -sin3-cos3 | B. | sin3-cos3 | C. | sin3+cos3 | D. | cos3-sin3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com